Unit 4.7: Transfer Functions for Circuit Analysis#

The preparatory reading for this section is Chapter 4.4 [Karris, 2012] which discusses transfer function models of electrical circuits. We have also adapted content from 3.6 The System Function from [Hsu, 2020].

Follow along at cpjobling.github.io/eg-150-textbook/laplace_transform/7/tf_for_circuits

QR Code for this lecture

Agenda#

In this unit, we will explore how transfer functions introduced in Unit 4.6: Transfer Functions can be applied to the analysis of circuits.

% Initialize MATLAB
clearvars
cd ../matlab 
format compact

Transfer Functions for Circuits#

When doing circuit analysis with components defined in the complex frequency domain, the ratio of the output voltage \(V_{\mathrm{out}}(s)\) to the input voltage \(V_{\mathrm{in}}(s)\) under zero initial conditions is of great interest.

This ratio is known as the voltage transfer function denoted \(G_v(s)\):

\[G_v(s) = \frac{V_{\mathrm{out}}(s)}{V_{\mathrm{in}}(s)}\]

Similarly, the ratio of the output current \(I_{\mathrm{out}}(s)\) to the input current \(I_{\mathrm{in}}(s)\) under zero initial conditions, is called the current transfer function denoted \(G_i(s)\):

\[G_i(s) = \frac{I_{\mathrm{out}}(s)}{I_{\mathrm{in}}(s)}\]

In practice, the current transfer function is rarely used, so we will use the voltage transfer function denoted:

\[G(s) = \frac{V_{\mathrm{out}}(s)}{V_{\mathrm{in}}(s)}\]

Exercises 14#

We will work through these and demonstrate the MATLAB solutions in class.

Exercise 14.1#

Derive an expression for the transfer function \(G(s)\) for the circuit shown in Fig. 69.

In this circuit \(R_g\) represents the internal resistance of the applied (voltage) source \(v_s\), and \(R_L\) represents the resistance of the load that consists of \(R_L\), \(L\) and \(C\).

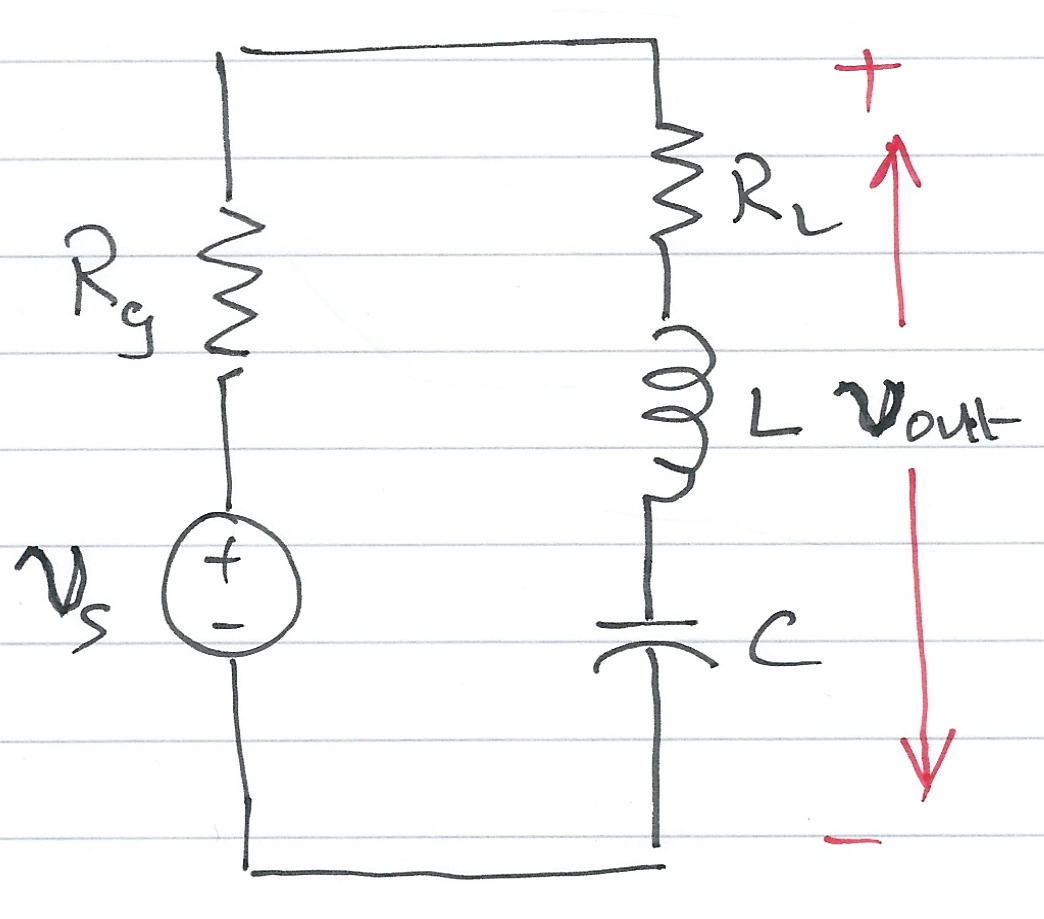
Circuit for Example 14.1

Fig. 69 Circuit for Example 14.1#

Sketch of Solution for Example 14.1#

  • Replace \(v_s(t)\), \(R_g\), \(R_L\), \(L\) and \(C\) by their transformed (complex frequency) equivalents: \(V_s(s)\), \(R_g\), \(R_L\), \(sL\) and \(1/(sC)\)

  • Use the Voltage Divider Rule to determine \(V_\mathrm{out}(s)\) as a function of \(V_s(s)\)

  • Form \(G(s)\) by writing down the ratio \(V_\mathrm{out}(s)/V_s(s)\)

Have a go for the next five minutes.

Worked solution for Example 14.1#

Pencast: ex6.pdf - open in Adobe Acrobat Reader.

Answer for Example 14.1#

\[G(s) = \frac{V_\mathrm{out}(s)}{V_s(s)} = \frac{R_L + sL + 1/sC}{R_g + R_L + sL + 1/sC}.\]

Exercise 14.2#

MATLAB Example

This is based on Example 4.7 from [Karris, 2012].

This is the basis for the mini project in MATLAB Lab 5.

Compute the transfer function for the op-amp circuit shown in Fig. 70 in terms of the circuit constants \(R_1\), \(R_2\), \(R_3\), \(C_1\) and \(C_2\).

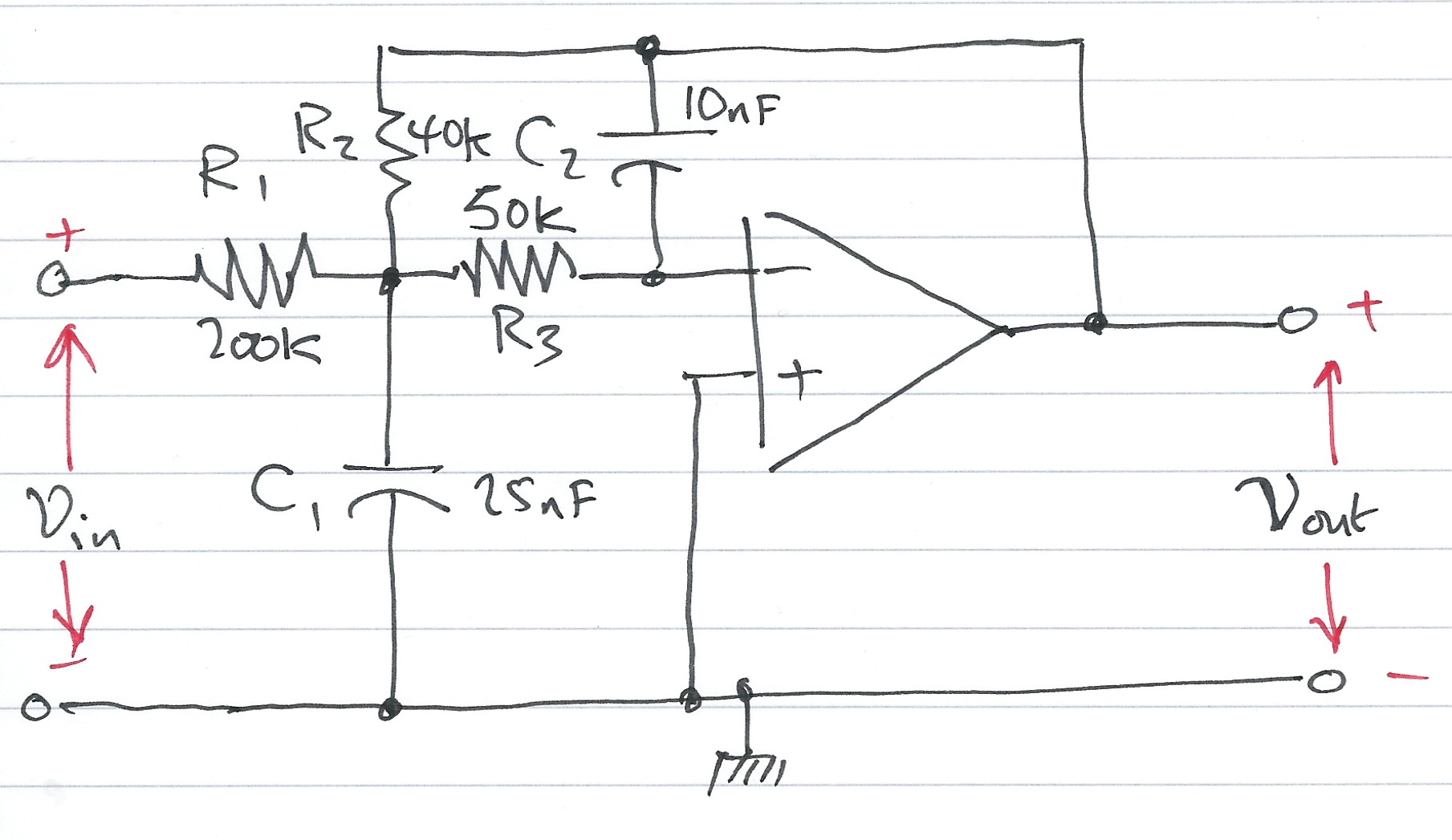
OpAmp circuit for Example 14.2

Fig. 70 OpAmp circuit for Example 14.2#

Then replace the complex variable \(s\) with \(j\omega\), and the circuit constants with their numerical values and plot the magnitude

\[\left|G(j\omega)\right| = \frac{\left|V_{\mathrm{out}}(j\omega)\right|}{\left|V_{\mathrm{in}}(j\omega)\right|}\]

versus radian frequency \(\omega\) rad/s.

Sketch of Solution for Example 14.2#

  • Replace the components and voltages in the circuit diagram with their complex frequency equivalents

  • Use nodal analysis to determine the voltages at the nodes either side of the 50K resistor \(R_3\)

Sketch of Solution for Example 14.2 (continued)#

  • Note that the voltage at the input to the op-amp is a virtual ground

  • Solve for \(V_{\mathrm{out}}(s)\) as a function of \(V_{\mathrm{in}}(s)\)

  • Form the reciprocal \(G(s) = V_{\mathrm{out}}(s)/V_{\mathrm{in}}(s)\)

Have a go for the next five minutes

Answer for Example 14.2#

(41)#\[G(s) = \frac{V_\mathrm{out}(s)}{V_\mathrm{in}(s)} = \frac{-1}{R_1\left(\left(1/R_1 + 1/R_2 + 1/R_3 + sC_1\right)\left(sC_2R_3\right)+1/R_2\right)}.\]

Worked solution for Example 14.2#

Pencast: ex7.pdf - open in Adobe Acrobat Reader.

Sketch of Solution for Example 14.2 (continued)#

  • Use MATLAB to calculate the component values, then replace \(s\) by \(j\omega\).

  • Compute \(\left|G(j\omega)\right|\) and plot on log-linear “paper”.

The MATLAB Bit#

Set up the symbols we will be using. In this case just the Laplace complex frequency \(s\).

syms s

Now define the values of the components

R1 = 200*10^3; 
R2 = 40*10^3;
R3 = 50*10^3;

C1 = 25*10^(-9);
C2 = 10*10^(-9);

Define the transfer function derived from analysis (Eq. (41))

den = R1*((1/R1+ 1/R2 + 1/R3 + s*C1)*(s*R3*C2) + 1/R2)

den =

100*s*((7555786372591433*s)/302231454903657293676544 + 1/20000) + 5

Simplify coefficients of \(s\) in the denominator. Note sym2poly converts a symbolic polynomial with numerical coeficients into a MATLAB polynomial.

format long
denH = sym2poly(den)

denH =
   0.000002500000000   0.005000000000000   5.000000000000000

Now define the numerator

numH = -1;

Plot the frequency response

For convenience, define coefficients \(a\) and \(b\):

a = denH(1);
b = denH(2);
\[G(j\omega) = \frac{-1}{a\omega^2 - jb\omega + 5}\]
w = 1:10:10000;
Hw = -1./(a*w.^2 - j.*b.*w + denH(3));

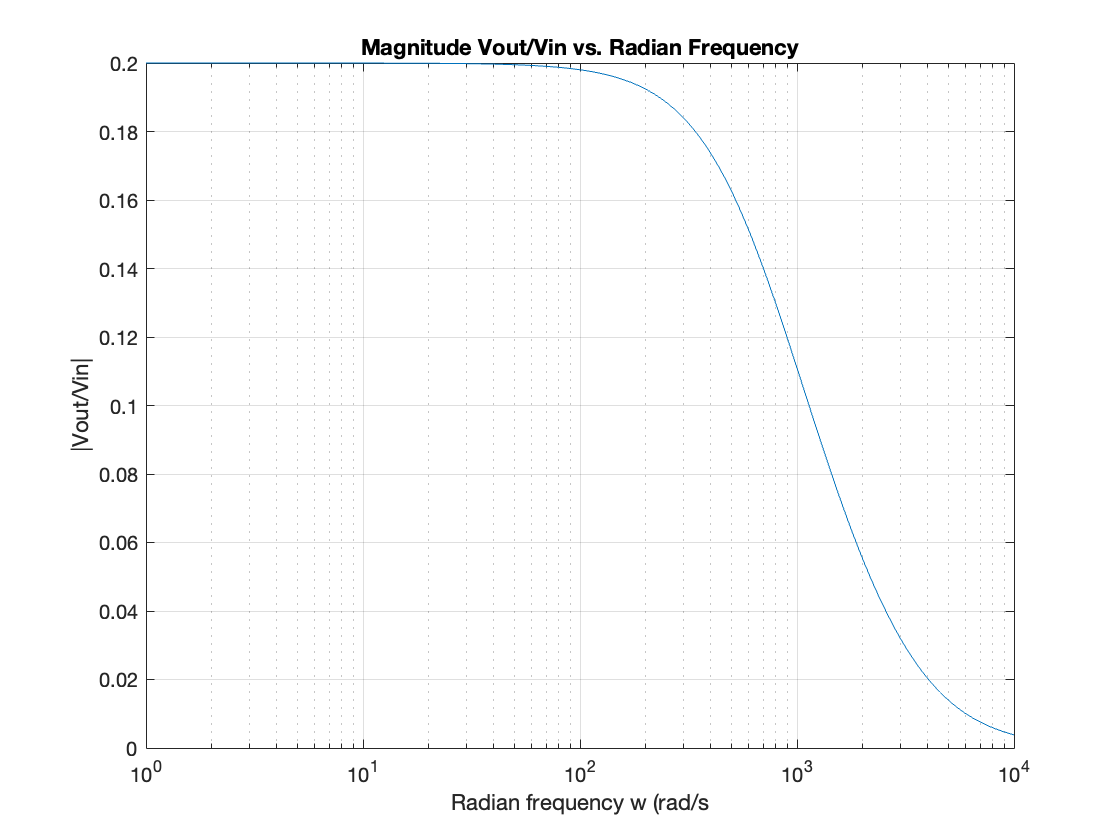
Plot \(|H(j\omega)|\) against \(\omega\) on log-lin “graph paper”.

semilogx(w, abs(Hw))
xlabel('Radian frequency w (rad/s')
ylabel('|Vout/Vin|')
title('Magnitude Vout/Vin vs. Radian Frequency')
grid
../../_images/737f08b0ddaabb4ece6bd7a357ab09b7151d911ddb618d40391d06916182c0c3.png

Note

Note that this is a low-pass filter. Sinusoids at low frequencies are passed with a gain of 0.2. For frequencies above around 100 rad/s, the filter starts to increase the attenuation of the passed signal. At 10,000 rad/s, the attenuation is 1/10 of the attenuation at 1 rad/s.

MATLAB Solutions#

For convenience, single script MATLAB solutions to the examples are provided and can be downloaded from the accompanying MATLAB folder.

Summary#

In this unit, we will explored how transfer functions introduced in Unit 4.6: Transfer Functions can be applied to the analysis of circuits.

Unit 4.7: Take Away#

The ratio of the output voltage \(V_\mathrm{out}(s)\) to the input voltage \(V_\mathrm{in}(s)\) under zero initial conditions is of great interest. We call this ratio the voltage transfer function

\[G_v(s) = \frac{V_\mathrm{out}(s)}{V_\mathrm{in}(s)}\]

We can consider other ratios such as the current transfer function

\[G_i(s) = \frac{I_\mathrm{out}(s)}{I_\mathrm{in}(s)}\]

but in practice this is rarely used.

Next time#

We explore the facilties provided by other toolboxes in MATLAB, most notably the Control Systems Toolbox and the simulation tool Simulink in Unit 4.8: Computer-Aided Systems Analysis and Simulation. We will also look at some of the problems you have studied in EG-152 Analogue Design hopefully confirming some of the results you have obbserved in the lab.

References#

Hsu20

Hwei P. Hsu. Schaums outlines signals and systems. McGraw-Hill, New York, NY, 2020. ISBN 9780071634724. Available as an eBook. URL: https://www.accessengineeringlibrary.com/content/book/9781260454246.

Kar12(1,2)

Steven T. Karris. Signals and systems with MATLAB computing and Simulink modeling. Orchard Publishing, Fremont, CA., 2012. ISBN 9781934404232. Library call number: TK5102.9 K37 2012. URL: https://ebookcentral.proquest.com/lib/swansea-ebooks/reader.action?docID=3384197.