Unit 5.3: The Inverse Z-Transform#

Colophon#

An annotatable worksheet for this presentation is available as Worksheet 10.

Scope and Background Reading#

This session we will talk about the Inverse Z-Transform and illustrate its use through an examples class.

The material in this presentation and notes is based on Chapter 9 (Starting at Section 9.6) of [Karris, 2012].

Agenda#

  • Inverse Z-Transform

  • Examples using PFE

  • Examples using Long Division

  • Analysis in MATLAB

Performing the Inverse Z-Transform#

The inverse Z-Transform enables us to extract a sequence \(f[n]\) from \(F(z)\). It can be found by any of the following methods:

  • Partial fraction expansion

  • The inversion integral

  • Long division of polynomials

Partial fraction expansion#

We expand \(F(z)\) into a summation of terms whose inverse is known. These terms have the form:

\[k,\;\frac{r_1 z}{z - p_1},\;\frac{r_1 z}{(z - p_1)^2},\;\frac{r_3 z}{z - p_2},\ldots\]

where \(k\) is a constant, and \(r_i\) and \(p_i\) represent the residues and poles respectively, and can be real or complex1.

Notes

  1. If complex, the poles and residues will be in complex conjugate pairs

\[\frac{r_{i} z}{z - p_i} + \frac{r_{i}^* z}{z - p_i^*}\]

Step 1: Make Fractions Proper#

  • Before we expand \(F(z)\) into partial fraction expansions, we must first express it as a proper rational function.

  • This is done by expanding \(F(z)/z\) instead of \(F(z)\)

  • That is we expand

\[\frac{F(z)}{z} = \frac{k}{z} + \frac{r_1}{z-p_1} + \frac{r_2}{z-p_2} + \cdots\]

Step 2: Find residues#

  • Find residues from

\[r_k = \lim_{z\to p_k}(z - p_k)\frac{F(z)}{z} = (z - p_k)\left.\frac{F(z)}{z}\right|_{z=p_k}\]

Step 3: Map back to transform tables form#

  • Rewrite \(F(z)/z\):

\[z\frac{F(z)}{z} = F(z) = k + \frac{r_1z}{z-p_1} + \frac{r_2z}{z-p_2} + \cdots\]

We will work through an example in class.

[Skip next slide in Pre-Lecture]

Example 1#

Karris Example 9.4: use the partial fraction expansion to compute the inverse z-transform of

\[F(z) = \frac{1}{(1 - 0.5z^{-1})(1 - 0.75z^{-1})(1 - z^{-1})}\]

MATLAB solution for example 1#

See example1.mlx. (Also available as example1.m.)

Uses MATLAB functions:

  • collect – expands a polynomial

  • sym2poly – converts a polynomial into a numeric polymial (vector of coefficients in descending order of exponents)

  • residue – calculates poles and zeros of a polynomial

  • ztrans – symbolic z-transform

  • iztrans – symbolic inverse z-transform

  • stem – plots sequence as a “lollipop” diagram

clear all
cd matlab
format compact

open example1

syms z n
assume(n,'integer')

The denoninator of \(F(z)\)

Dz = (z - 0.5)*(z - 0.75)*(z - 1);

Multiply the three factors of Dz to obtain a polynomial

Dz_poly = collect(Dz)

Dz_poly =

z^3 - (9*z^2)/4 + (13*z)/8 - 3/8

Make into a rational polynomial#

\(z^2\)

num = [0, 1, 0, 0];

\(z^3 - 9/4 z^2 - 13/8 z - 3/8\)

den = sym2poly(Dz_poly)

den =
    1.0000   -2.2500    1.6250   -0.3750

Compute residues and poles#

[r,p,k] = residue(num,den);

Symbolic proof#

\[f[n] = 2\left(\frac{1}{2}\right)^n - 9\left(\frac{3}{4}\right)^n + 8\]
% z-transform
fn = 2*(1/2)^n-9*(3/4)^n + 8;
Fz = ztrans(fn)

Fz =

(8*z)/(z - 1) + (2*z)/(z - 1/2) - (9*z)/(z - 3/4)

% inverse z-transform
iztrans(Fz)

ans =

2*(1/2)^n - 9*(3/4)^n + 8

Sequence#

n = 0:15;
sequence = subs(fn,n);
stem(n,sequence)
title('Discrete Time Sequence f[n] = 2*(1/2)^n-9*(3/4)^n + 8');
ylabel('f[n]')
xlabel('Sequence number n')
../../_images/ac810fd3e83ae840ef57dc89f1b8c8adf19f549cca5c477eb88d6e8540c10c5a.png

Example 2#

Karris example 9.5: use the partial fraction expansion method to to compute the inverse z-transform of

\[F(z) = \frac{12z}{(z+1)(z - 1)^2}\]

MATLAB solution for example 2#

See example2.mlx. (Also available as example2.m.)

Uses additional MATLAB functions:

  • dimpulse – computes and plots a sequence \(f[n]\) for any range of values of \(n\)

open example2

Results for example 2#

‘Lollipop’ Plot#

Results for example 2 - lollipop plot

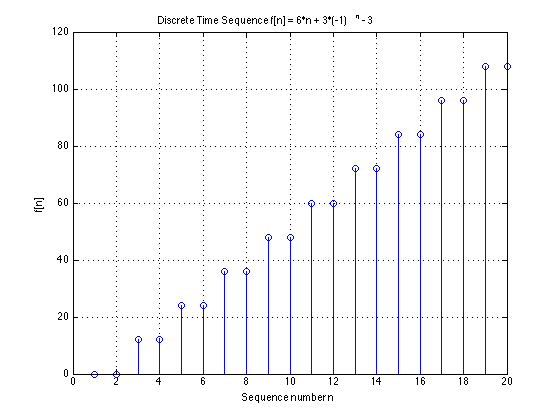
‘Staircase’ Plot#

Simulates output of Zero-Order-Hold (ZOH) or Digital Analogue Converter (DAC)

Results for example 2 - staircase plot

Example 3#

Karris example 9.6: use the partial fraction expansion method to to compute the inverse z-transform of

\[F(z) = \frac{z + 1}{(z-1)(z^2 + 2z + 2)}\]

MATLAB solution for example 3#

See example3.mlx. (Also available as example3.m.)

open example3

Results for example 3#

Lollipop Plot#

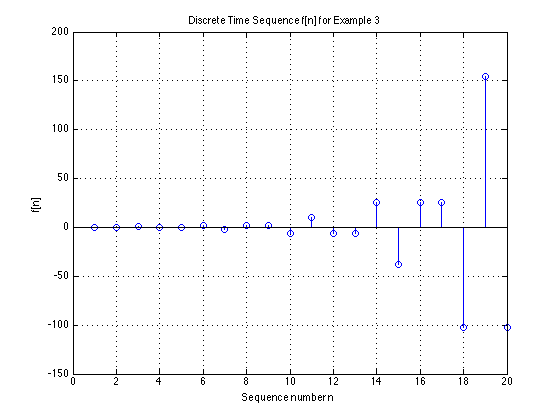
Results for example 3 - lollipop plot

Staircase Plot#

Results for example 3 - staircase plot

Inverse Z-Transform by the Inversion Integral#

The inversion integral states that:

\[f[n] = \frac{1}{j2\pi}\oint_C {F(z){z^{n - 1}}\,dz} \]

where \(C\) is a closed curve that encloses all poles of the integrant.

This can (apparently) be solved by Cauchy’s residue theorem!!

Fortunately (:-), this is beyond the scope of this module!

See Karris Section 9.6.2 (pp 9-29—9-33) if you want to find out more.

Inverse Z-Transform by the Long Division#

To apply this method, \(F(z)\) must be a rational polynomial function, and the numerator and denominator must be polynomials arranged in descending powers of \(z\).

We will work through an example in class.

[Skip next slide in Pre-Lecture]

Example 4#

Karris example 9.9: use the long division method to determine \(f[n]\) for \(n = 0,\,1,\,\mathrm{and}\,2\), given that

\[F(z) = \frac{1 + z^{-1} + 2z^{-2} + 3z^{-3}}{(1 - 0.25z^{-1})(1 - 0.5z^{-1})(1 - 0.75z^{-1})}\]

MATLAB solution for example 4#

See example4.mlx. (also available as example4.m.)

open example4

Results for example 4#

sym_den =
 
z^3 - (3*z^2)/2 + (11*z)/16 - 3/32
 

fn =

    1.0000
    2.5000
    5.0625
    ....

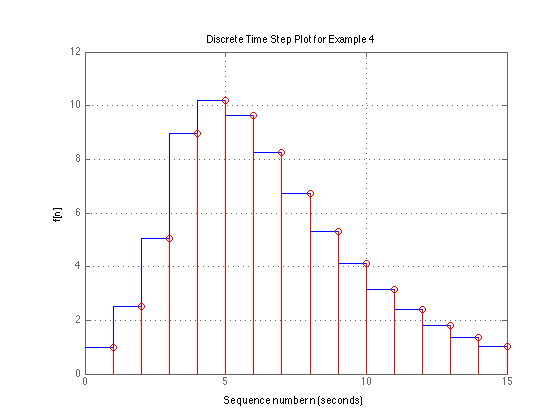
Combined Staircase/Lollipop Plot#

Combined Staircase/Lollipop Plot

Methods of Evaluation of the Inverse Z-Transform#

Partial Fraction Expansion#

Advantages

  • Most familiar.

  • Can use MATLAB residue function.

Disadvantages

  • Requires that \(F(z)\) is a proper rational function.

Inversion Integral#

Advantage

  • Can be used whether \(F(z)\) is rational or not

Disadvantages

  • Requires familiarity with the Residues theorem of complex variable analaysis.

Long Division#

Advantages

  • Practical when only a small sequence of numbers is desired.

  • Useful when z-transform has no closed-form solution.

Disadvantages

  • Can use MATLAB dimpulse function to compute a large sequence of numbers.

  • Requires that \(F(z)\) is a proper rational function.

  • Division may be endless.

Summary#

  • Inverse Z-Transform

  • Examples using PFE

  • Examples using Long Division

  • Analysis in MATLAB

Coming Next

  • DT transfer functions, continuous system equivalents, and modelling DT systems in Matlab and Simulink.

Reference#

See Bibliography.

Answers to Examples#

Answer to Example 1#

\[f[n] = 2\left(\frac{1}{2}\right)^n - 9\left(\frac{3}{4}\right)^n + 8\]

Answer to Example 2#

\[f[n] = 3(-1)^n + 6n - 3\]

Answer to Example 3#

\[f[n] = -0.5\delta[n] + 0.4 + \frac{(\sqrt{2})^n}{10}\cos \left(\frac{3n\pi}{4}\right) - \frac{3(\sqrt{2})^n}{10}\sin\left( \frac{3n\pi}{4}\right)\]

Answer to Example 4#

\(f[0] = 1\), \(f[1] = 5/2\), \(f[2] = 81/16\), ….

Worked solutions#