Unit 3.2: Exponential Fourier Series

Unit 3.2: Exponential Fourier Series#

Colophon#

An annotatable worksheet for this presentation is available as Worksheet 3.

The source code for this page is fourier_series/2/exp_fs1.md.
You can view the notes for this presentation as a webpage (Unit 3.2: Exponential Fourier Series).
This page is downloadable as a PDF file.

This section builds on our study of Unit 3.1: Trigonometric Fourier Series.

Trigonometric Fourier series uses integration of a periodic signal multiplied by sines and cosines at the fundamental and harmonic frequencies. If performed by hand, this can a painstaking process. Even with the simplifications made possible by exploiting waveform symmetries, there is still a need to integrate cosine and sine terms, be aware of and able to exploit the trigonometrc identities, and the properties of orthogonal functions before we can arrive at the simplified solutions. This is why I concentrated on the properties and left the computation to a computer.

However, by exploiting the exponential function $e^{a t}$ , we can derive a method for calculating the coefficients of the harmonics that is much easier to calculate by hand and converted into an algorithm that can be executed by computer.

The result is called the Exponential Fourier Series.

Agenda#

Exponents and Euler’s Equation
The Exponential Fourier series
Symmetry in Exponential Fourier Series
Example

The Exponential Function $e^{a t}$ #

You should already be familiar with $e^{a t}$ because it appears in the solution of differential equations.
It is also a function that appears in the definition of the Laplace and Inverse Laplace Transform.
It pops up again and again in tables and properies of the Laplace Transform.

Case when a is real.#

When $a$ is real the function $e^{a t}$ will take one of the two forms illustrated below:

clear all
setappdata(0, "MKernel_plot_format", 'svg')

%% The decaying exponential
t=linspace(-1,2,1000);
figure
plot(t,exp(t),t,exp(0.*t),t,exp(-t))
axis([-1,2,-1,8])
title('exp(at) -- a real')
xlabel('t (s)')
ylabel('exp(t) and exp(-t)')
legend('exp(t)','exp(0)','exp(-t)')
grid
hold off

You can regenerate this image generated with this Matlab script: expon.m.

When $a < 0$ the response is a decaying exponential (red line in plot)
When $a = 0$ $e^{a t} = 1$ – essentially a model of DC
When $a > 0$ the response is an unbounded increasing exponential (blue line in plot)

Case when a is imaginary#

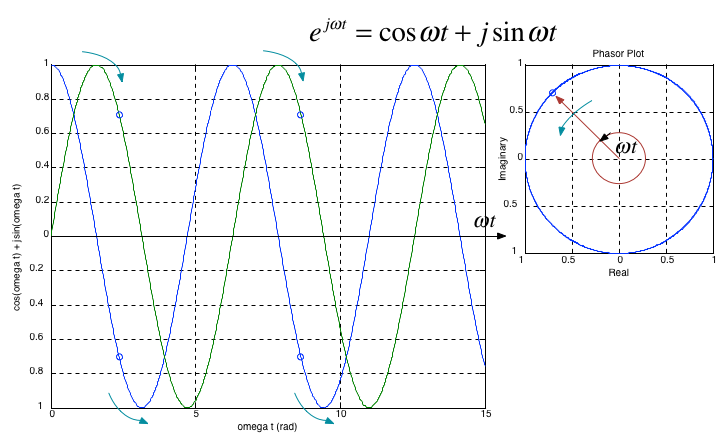
exp(j*omega*t) = cos(omega*t) + j*sin(omega*t)

This is the case that helps us to simplify the computation of sinusoidal Fourier series.

It was Leonhard Euler who discovered the formula visualized above.

Some important values of $ω t$ #

These are useful when simplifying expressions that result from integrating functions that involve the imaginary exponential

Give the following:

$e^{j ω t}$ when $ω t = 0$
$e^{j ω t}$ when $ω t = π / 2$
$e^{j ω t}$ when $ω t = π$
$e^{j ω t}$ when $ω t = 3 π / 2$
$e^{j ω t}$ when $ω t = 2 π$

Case where $a$ is complex#

We shall not say much about this case except to note that the Laplace transform equation includes such a number. The variable $s$ in the Laplace Transform

\int_{0}^{\infty} f (t) e^{- s t} d t

is a complex exponential.

The consequences of a complex $s$ have particular significance in the development of system stability theories and in control systems analysis and design. Look out for them in EG-243.

Two Other Important Properties#

By use of trig. identities, it is relatively straight forward to show that:

\cos ω t = \frac{e^{j ω t} + e^{- j ω t}}{2}

and

\sin ω t = \frac{e^{j ω t} - e^{- j ω t}}{j 2}

We can use this result to convert the Trigonometric Fourier Series into an Exponential Fourier Series which has only one integral term to solve per harmonic.

The Exponential Fourier Series#

As as stated in the notes on the Trigonometric Fourier Series any periodic waveform $f (t)$ can be represented as

\begin{array}{r} \begin{array}{c} f (t) = \frac{1}{2} a_{0} + a_{1} \cos Ω_{0} t + a_{2} \cos 2 Ω_{0} t + \dots \\ + b_{1} \sin Ω_{0} t + b_{2} \sin 2 Ω_{0} t + \dots \end{array} \end{array}

Let us replace the $\cos$ and $\sin$ terms with their imaginary exponential equivalents:

\begin{array}{r} \begin{array}{c} f (t) = \frac{1}{2} a_{0} + a_{1} (\frac{e^{j Ω_{0} t} + e^{- j Ω_{0} t}}{2}) + a_{2} (\frac{e^{j 2 Ω_{0} t} + e^{- j 2 Ω_{0} t}}{2}) + \dots \\ + b_{1} (\frac{e^{j Ω_{0} t} - e^{- j Ω_{0} t}}{j 2}) + b_{2} (\frac{e^{j 2 Ω_{0} t} - e^{- j 2 Ω_{0} t}}{j 2}) + \dots \end{array} \end{array}

Grouping terms with same exponents#

f (t) = \dots + (\frac{a_{2}}{2} - \frac{b_{2}}{j 2}) e^{- j 2 Ω_{0} t} + (\frac{a_{1}}{2} - \frac{b_{1}}{j 2}) e^{- j Ω_{0} t} + \frac{1}{2} a_{0} + (\frac{a_{1}}{2} + \frac{b_{1}}{j 2}) e^{j Ω_{0} t} + (\frac{a_{2}}{2} + \frac{b_{2}}{j 2}) e^{j 2 Ω_{0} t} + \dots

New coefficients#

The terms in parentheses are usually denoted as

C_{- k} = \frac{1}{2} (a_{k} - \frac{b_{k}}{j}) = \frac{1}{2} (a_{k} + j b_{k})

C_{k} = \frac{1}{2} (a_{k} + \frac{b_{k}}{j}) = \frac{1}{2} (a_{k} - j b_{k})

C_{0} = \frac{1}{2} a_{0}

The Exponential Fourier Series is

f (t) = \dots + C_{- 2} e^{- j 2 Ω_{0} t} + C_{- 1} e^{- j Ω_{0} t} + C_{0} + C_{1} e^{j Ω_{0} t} + C_{2} e^{j 2 Ω_{0} t} + \dots

or more compactly

f (t) = \sum_{k = - n}^{n} C_{k} e^{j k Ω_{0} t}

Important

The $C_{k}$ coefficents, except for $C_{0}$ are complex and appear in conjugate pairs so

C_{- k} = C_{k}^{*}

Evaluation of the complex coefficients#

The coefficients are obtained from the following expressions:

C_{k} = \frac{1}{2 π} \int_{0}^{2 π} f (Ω_{0} t) e^{- j k (Ω_{0} t)} d (Ω_{0} t) = \frac{1}{2 π} \int_{0}^{2 π} f (θ) e^{- j k θ} d θ

or

C_{k} = \frac{1}{T} \int_{0}^{T} f (t) e^{- j k Ω_{0} t} d t

These are much easier to derive and compute than the equivalent Trigonemetric Fourier Series coefficients[1].

Trigonometric Fourier Series from Exponential Fourier Series#

By substituting $C_{- k}$ and $C_{k}$ back into the original expansion

C_{k} + C_{- k} = \frac{1}{2} (a_{k} - j b_{k} + a_{k} + j b_{k})

so

a_{k} = C_{k} + C_{- k}

Similarly

C_{k} - C_{- k} = \frac{1}{2} (a_{k} - j b_{k} - a_{k} - j b_{k})

so

b_{k} = j (C_{k} - C_{- k})

Thus, we can easily go back to the trigonometric Fourier series if we need to.

Symmetry in exponential Fourier series#

Since the coefficients of the exponential Fourier series are complex numbers, we can use symmetry to determine the form of the coefficients and thereby simplify the computation of series for wave forms that have symmetry.

Even Functions#

For even functions, all the coefficients $C_{k}$ are real.

Proof

Recall

C_{- k} = \frac{1}{2} (a_{k} - \frac{b_{k}}{j}) = \frac{1}{2} (a_{k} + j b_{k})

and

C_{k} = \frac{1}{2} (a_{k} + \frac{b_{k}}{j}) = \frac{1}{2} (a_{k} - j b_{k})

From knowledge of the trig. fourier series, even functions have no sine terms so the $b_{k}$ coefficients are 0. Therefore both $C_{- k}$ and $C_{k}$ are real.

Odd Functions#

For odd functions, all coefficients $C_{k}$ are imaginary.

By a similar argument, all odd functions have no cosine terms so the $a_{k}$ coefficients are 0. Therefore both $C_{- k}$ and $C_{k}$ are imaginary.

Half-wave symmetry#

If there is half-wave symmetry, $C_{k} = 0$ for $k$ even.

Proof

From trigonometric Fourier series, if there is half-wave symmetry, all even harnonics are zero, thus both $a_{k}$ and $b_{k}$ are zero for $k$ even. Hence $C_{- k}$ and $C_{k}$ are also zero when $k$ is even.

No symmetry#

If there is no symmetry the exponential Fourier series of $f (t)$ is complex.

Relation of $C_{- k}$ to $C_{k}$ #

$C_{- k} = C_{k}^{*}$ always

Example 1#

Compute the Exponential Fourier Series for the square wave shown below assuming that $ω = 1$

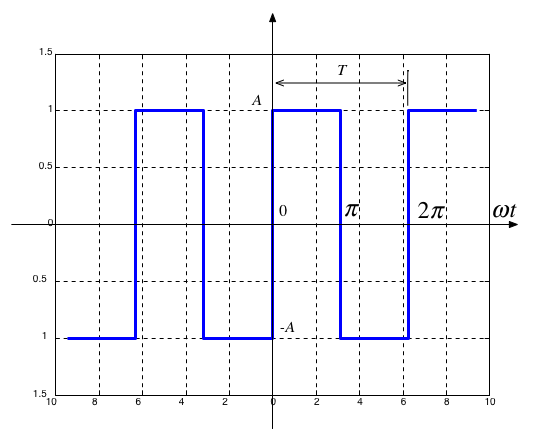
Will be solved by hand in Class#

Some questions for you#

Square wave is an [odd/even/neither] function?
DC component is [zero/non-zero]?
Square wave [has/does not have] half-wave symmetry?

Hence

$C_{0} =$ [?]
Coefficients $C_{k}$ are [real/imaginary/complex]?
Subscripts $k$ are [odd only/even only/both odd and even]?
What is the integral that needs to be solved for $C_{k}$ ?

Solution to example 1#

The integral is

C_{k} = \frac{1}{2 π} \int_{0}^{2 π} f (Ω_{0} t) e^{- j k (Ω_{0} t)} d (Ω_{0} t) = \frac{1}{2 π} [\int_{0}^{π} A e^{- j k (Ω_{0} t)} d (Ω_{0} t) + \int_{π}^{2 π} (- A) e^{- j k (Ω_{0} t)} d (Ω_{0} t)]

For simplicity let $θ = Ω_{0} t$ .

\frac{1}{2 π} [\int_{0}^{π} A e^{- j k θ} d θ + \int_{π}^{2 π} (- A) e^{- j k θ} d θ] = \frac{1}{2 π} [{\frac{A}{- j k} e^{- j k θ} |}_{0}^{π} + {\frac{- A}{- j k} e^{- j k θ} |}_{π}^{2 π}]

= \frac{1}{2 π} [\frac{A}{- j k} (e^{- j k π} - 1) + \frac{A}{j k} (e^{- j 2 k π} - e^{- j k π})] = \frac{A}{2 j π k} (1 - e^{- j k π} + e^{- j 2 k π} - e^{- j k π})

\frac{A}{2 j π k} (e^{- j 2 k π} - 2 e^{- j k π} - 1) = \frac{A}{2 j π k} {(e^{- j k π} - 1)}^{2}

For $n$ odd[2], $e^{- j k π} = - 1$ . Therefore

\binom{C_{k}}{k = odd} = \frac{A}{2 j π k} {(e^{- j k π} - 1)}^{2} = \frac{A}{2 j π k} {(- 1 - 1)}^{2} = \frac{A}{2 j π k} {(- 2)}^{2} = \frac{2 A}{j π k}

\binom{C_{k}}{k = even} = 0.

Exponential Fourier series for the square wave with odd symmetry#

From the definition of the exponential Fourier series

f (t) = \dots + C_{- 2} e^{- j 2 Ω_{0} t} + C_{- 1} e^{- j Ω_{0} t} + C_{0} + C_{1} e^{j Ω_{0} t} + C_{2} e^{j 2 Ω_{0} t} + \dots

the exponential Fourier series for the square wave with odd symmetry is

f (t) = \frac{2 A}{j π} (\dots - \frac{1}{3} e^{- j 3 Ω_{0} t} - e^{- j Ω_{0} t} + e^{j Ω_{0} t} + \frac{1}{3} e^{j 3 Ω_{0} t} + \dots) = \frac{2 A}{j π} \sum_{k = odd} \frac{1}{k} e^{j k Ω_{0} t}

Note the sign change in first two terms. This is due to the fact that $C_{- k} = C_{k}^{*}$ .

E.g. since $C_{3} = 2 A / j 3 π$ , $C_{- 3} = C_{3}^{*} = - 2 A / j 3 π$

Trig. Fourier series from exponential Fourier series#

Since

f (t) = \frac{2 A}{j π} (\dots - \frac{1}{3} e^{- j 3 Ω_{0} t} - e^{- j Ω_{0} t} + e^{j Ω_{0} t} + \frac{1}{3} e^{j 3 Ω_{0} t} + \dots)

gathering terms at each harmonic frequency gives

\begin{array}{r} \begin{array}{rcl} f (t) & = & \frac{4 A}{π} (\dots + (\frac{e^{j Ω_{0} t} - e^{- j Ω_{0} t}}{2 j}) + \frac{1}{3} (\frac{e^{j 3 Ω_{0} t} - e^{- j 3 Ω_{0} t}}{2 j}) + \dots) \\ = & \frac{4 A}{π} (\sin Ω_{0} t + \frac{1}{3} \sin 3 Ω_{0} t + \dots) \\ = & \frac{4 A}{π} \sum_{k = odd} \frac{1}{k} \sin k Ω_{0} t . \end{array} \end{array}

Computing coefficients of Exponential Fourier Series in MATLAB#

Example 2#

Verify the result of Example 1 using MATLAB.

Solution to example 2#

Solution: See efs_sqw.m.

EFS_SQW#

Calculates the Exponential Fourier for a Square Wave with Odd Symmetry.

cd ../matlab
format compact; 
setappdata(0, "MKernel_plot_format", 'svg')

Set up parameters

syms t A;

tau = 1;
T0 = 2*pi; % w = 2*pi*f -> t = 2*pi/omega
k_vec = [-5:5];

Define f(t)

IMPORTANT: the signal definition must cover [0 to T0]

xt = A*(heaviside(t)-heaviside(t-T0/2)) - A*(heaviside(t-T0/2)-heaviside(t-T0));

Compute EFS

[X, w] = FourierSeries(xt, T0, k_vec)

Plot the numerical results from MATLAB calculation.

Convert symbolic to numeric result

Xw = subs(X,A,1);

Plot

subplot(211)
stem(w,abs(Xw), 'o-');
title('Exponential Fourier Series for Square Waveform with Odd Symmetry')
xlabel('Hamonic frequencies: k\Omega_0 (rad/sec)');
ylabel('|c_k|');
subplot(212)
stem(w,angle(Xw), 'o-');
xlabel('Hamonic frequencies: k\Omega_0 (rad/sec)');
ylabel('\angle c_k [radians]');

Summary#

Exponents and Euler’s Equation
The exponential Fourier series
Symmetry in Exponential Fourier Series
Example

Answers to in-class problems#

Some important values of $ω t$ - Solution#

When $ω t = 0$ : $e^{j ω t} = e^{j 0} = 1$
When $ω t = π / 2$ : $e^{j ω t} = e^{j π / 2} = j$
When $ω t = π$ : $e^{j ω t} = e^{j π} = - 1$
When $ω t = 3 π / 2$ : $e^{j ω t} = e^{j 3 π / 2} = - j$
When $ω t = 2 π$ : $e^{j ω t} = e^{j 2 π} = e^{j 0} = 1$

It is also worth being aware that $n ω t$ , when $n$ is an integer, produces rotations that map back to the simpler cases given above. For example see $e^{j 2 π}$ above.

Some answers for you#

Square wave is an odd function!
DC component is zero!
Square wave has half-wave symmetry!