Worksheet 4#

To accompany Unit 3.3 Computing Line Spectra#

Colophon#

This worksheet can be downloaded as a PDF file. We will step through this worksheet in class.

An annotatable copy of the notes for this presentation will be distributed before the second class meeting as Worksheet 4 in the Week 4: Classroom Activities section of the Canvas site. I will also distribute a copy to your personal Worksheets section of the OneNote Class Notebook so that you can add your own notes using OneNote.

You are expected to have at least watched the video presentation of Unit 3.3: Computing Line Spectra of the notes before coming to class. If you haven’t watch it afterwards!

After class, the lecture recording and the annotated version of the worksheets will be made available through Canvas.

Example 3#

Compute the exponential Fourier series for the waveform shown below and plot its line spectra.

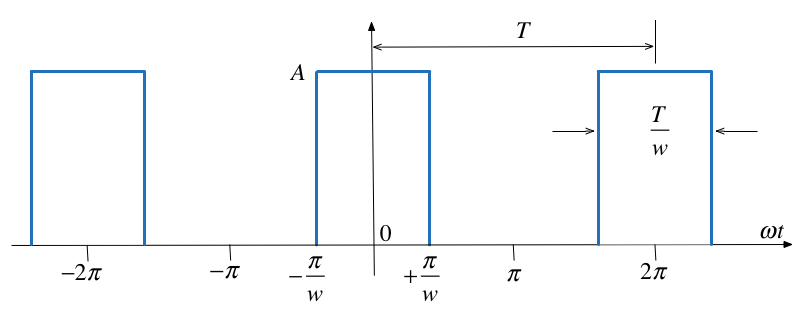
Solution to example 3#

The recurrent rectangular pulse is used extensively in digital communication systems. To determine how faithfully such pulses will be transmitted, it is necessary to know the frequency components.

What do we know?

  • The pulse duration is \(T/w\).

  • The recurrence interval \(T\) is \(w\) times the pulse duration.

  • \(w\) is the ratio of pulse repetition time to the pulse duration – normally called the duty cycle.

Coefficients of the Exponential Fourier Series?#

Given

\[C_k = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(\theta) e^{-jk\theta}\,d\theta\]

  • Is the function even or odd?

  • Does the signal have half-wave symmetry?

  • What are the consequencies of symmetry on the form of the coefficients \(C_k\)?

  • What function do we actually need to integrate to compute \(C_k\)?

DC Component?#

Let \(k = 0\) then perform the integral

Harmonic coefficients?#

Integrate for \(k\ne 0\)

Exponential Fourier Series?#

Effect of pulse width on frequency spectra#

  • Recall pulse width = \(T/w\)

We will use the provided MATLAB script sinc.mlx to explore these in class. You will also need pulse_fs.m. See Canvas/OneNote for copies of these files.

w = 2#

\(\Omega_0 = 1\) rad/s; \(w = 2\); \(T = 2\pi\) s; \(T/w = \pi\) s.

w = 5#

\(\Omega_0 = 1\) rad/s; \(w = 5\); \(T = 2\pi\) s; \(T/w = 2\pi/5\) s.

w = 10#

\(\Omega_0 = 1\) rad/s; \(w = 10\); \(T = 2\pi\) s; \(T/w = \pi/5\) s.

Implications#

  • As the width of the pulse reduces the width of the freqency spectra needed to fully describe the signal increases

  • more bandwidth is needed to transmit the pulse.

Example 4#

Use the result of Example 1 to compute the exponential Fourier series of the impulse train \(\delta(t\pm 2\pi k)\) shown below

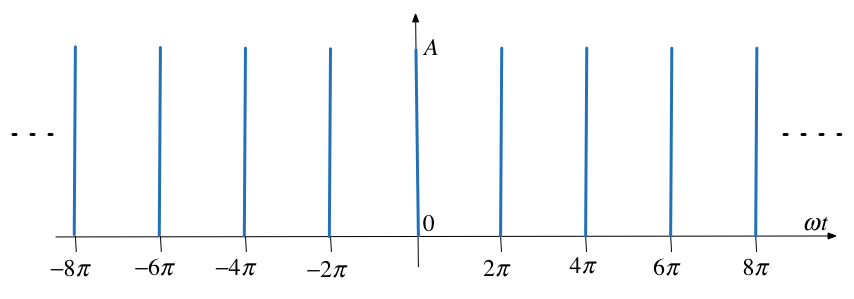
Solution to example 4#

To solve this we take the previous result and choose amplitude (height) \(A\) so that area of pulse is unity. Then we let width go to zero while maintaining the area of unity. This creates a train of impulses \(\delta(t\pm 2\pi k)\).

\[C_k = \frac{1}{2\pi}\]

and, therefore

\[f(t) = \frac{1}{2\pi}\sum_{k=-\infty}^{\infty} e^{jk\Omega_0 t}\]

Try it!

Proof!#

From the previous result,

\[C_k = \frac{A}{w}.\frac{\sin(k\pi/w)}{k\pi/w}\]

and the pulse width was defined as \(T/w\), that is

\[\frac{T}{w}=\frac{2\pi}{w}\]

Let us take the previous impulse train as a recurrent pulse with amplitude

\[A = \frac{1}{T/w} = \frac{1}{2\pi/w} = \frac{w}{2\pi}.\]

Pulse with unit area#

The area of each pulse is then

\[\frac{2\pi}{w}\times\frac{w}{2\pi} = 1\]

and the pulse train is as shown below:

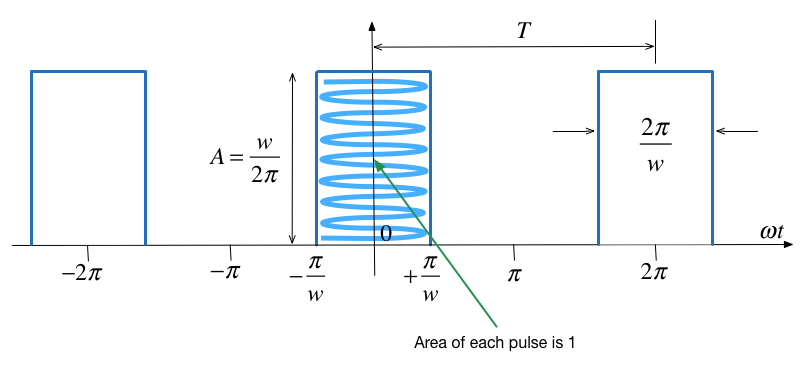
New coefficents#

The coefficients of the Exponential Fourier Series are now:

\[C_n = \frac{w/2\pi}{w}\frac{\sin(k\pi/w)}{k\pi/w} = \frac{1}{2\pi}\frac{\sin(k\pi/w)}{k\pi/w}\]

and as \(\pi/w \to 0\) each recurrent pulse becomes a unit impulse, and the pulse train reduces to a unit impulse train.

Also, recalling that

\[\lim_{x\to 0} \frac{sin x}{x} = 1\]

the coefficents reduce to

\[C_n = \frac{1}{2\pi}\]

That is all coefficients have the same amplitude and thus

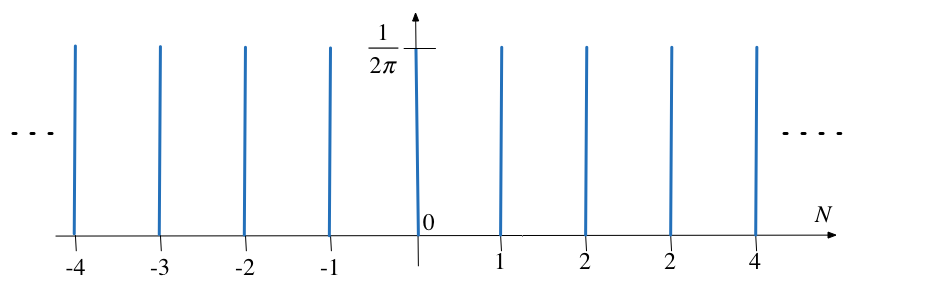
\[f(t) = \frac{1}{2\pi}\sum_{n=-\infty}^{\infty} e^{jk\Omega_0 t}\]

Spectrum of Unit Impulse Train#

The line spectrum of a sequence of unit impulses \(\delta(t \pm kT)\) is shown below:

Another Interesting Result#

Consider the pulse train agin:

What happens when the pulses to the left and right of the centre pulse become less and less frequent? That is what happens when \(T \to \infty\)?

Well?#

  • As \(T\to \infty\) the fundamental frequency \(\Omega_0 \to 0\)

  • We are then left with just one pulse centred around \(t=0\).

  • The frequency difference between harmonics also becomes smaller.

  • Line spectrum becomes a continous function.

This result is the basis of the Fourier Transform which is coming soon.