Unit 4.3: Fourier Transforms for Circuit and LTI Systems Analysis#

Colophon#

An annotatable worksheet for this presentation is available as Worksheet 8.

In this section we will apply what we have learned about Fourier transforms to some typical circuit problems. After a short introduction, the body of this chapter will form the basis of an examples class.

Agenda#

  • The system function

  • Examples

The System Function#

System response from the system impulse response#

Recall that the convolution integral of a system with impulse response \(h(t)\) and input \(u(t)\) is

\[h(t)*u(t)=\int_{-\infty}^{\infty}h(t-\tau)u(\tau)\,d\tau.\]

We let

\[g(t) = h(t)*u(t)\]

Then by the time convolution property

\[h(t)*u(t) = g(t) \Leftrightarrow G(\omega) = H(\omega).U(\omega)\]

The System Function#

We call \(H(\omega)\) the system function.

We note that the system function \(H(\omega)\) and the impulse response \(h(t)\) form the Fourier transform pair

\[h(t) \Leftrightarrow H(\omega)\]

Obtaining system response#

If we know the impulse resonse \(h(t)\), we can compute the system response \(g(t)\) of any input \(u(t)\) by multiplying the Fourier transforms of \(H(\omega)\) and \(U(\omega)\) to obtain \(G(\omega)\). Then we take the inverse Fourier transform of \(G(\omega)\) to obtain the response \(g(t)\).

  1. Transform \(h(t) \to H(\omega)\)

  2. Transform \(u(t) \to U(\omega)\)

  3. Compute \(G(\omega) = H(\omega).U(\omega)\)

  4. Find \(\mathcal{F}^{-1}\left\{G(\omega)\right\} \to g(t)\)

Examples#

Example 1#

Karris example 8.8: for the linear network shown below, the impulse response is \(h(t)=3e^{-2t}u_0(t)\). Use the Fourier transform to compute the response \(y(t)\) when the input \(u(t)=2[u_0(t)-u_0(t-3)]\). Verify the result with MATLAB.

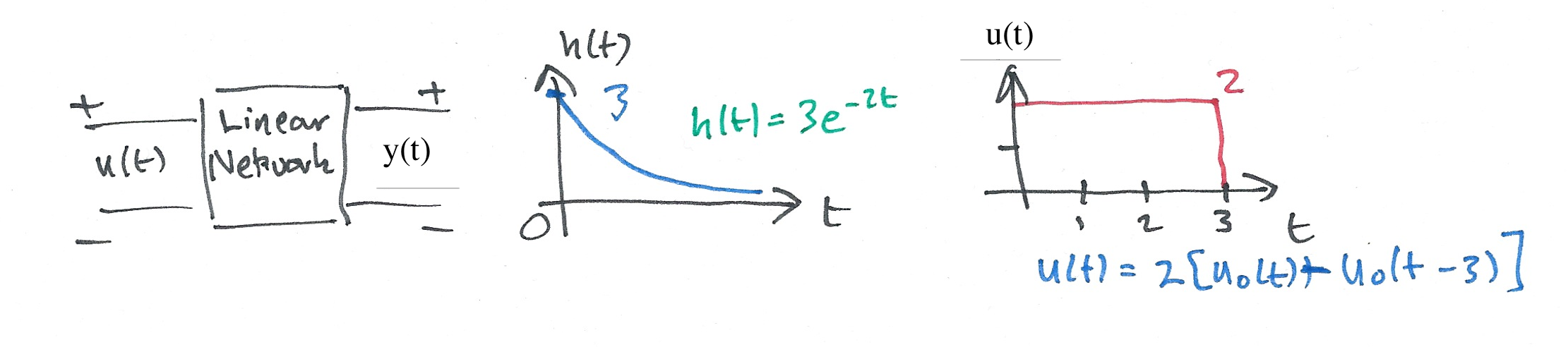
Example 1

Solutions see: Worked Solutions

MATLAB verification of example 1#

format compact; % reduce whitesace for textbook presentation
syms t w
U1 = fourier(2*heaviside(t),t,w)

U1 =

2*pi*dirac(w) - 2i/w

H = fourier(3*exp(-2*t)*heaviside(t),t,w)

H =

3/(2 + w*1i)

Y1=simplify(H*U1)

Y1 =

3*pi*dirac(w) - 6i/(w*(2 + w*1i))

y1 = simplify(ifourier(Y1,w,t))

y1 =

(3*exp(-2*t)*(sign(t) + 1)*(exp(2*t) - 1))/2

Get y2

Substitute \(t-3\) into \(t\).

y2 = subs(y1,t,t-3)

y2 =

(3*exp(6 - 2*t)*(sign(t - 3) + 1)*(exp(2*t - 6) - 1))/2

y = y1 - y2

y =

(3*exp(-2*t)*(sign(t) + 1)*(exp(2*t) - 1))/2 - (3*exp(6 - 2*t)*(sign(t - 3) + 1)*(exp(2*t - 6) - 1))/2

The result is equivalent to:

y = 3*heaviside(t) - 3*heaviside(t - 3) + 3*heaviside(t - 3)*exp(6 - 2*t) - 3*exp(-2*t)*heaviside(t)

Which after gathering terms gives

\[y(t) = 3(1 - 3e^{-2t})u_0(t) - 3(1 - 3e^{-2(t-3)})u_0(t-3)\]

Plot result

fplot(y,[0,6])
title('Solution to Example 1')
ylabel('y(t)')
xlabel('t [s]')
grid
../../_images/905dd49c8ee85ae275381ea2daca17fe9e11b07c3355b5b5eeaa58d0ee543869.png

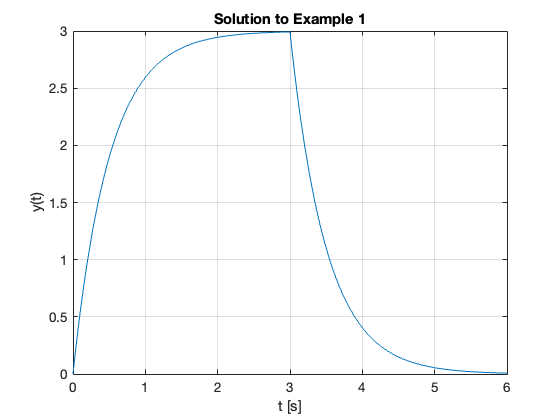
Example 2#

Karris example 8.9: for the circuit shown below, use the Fourier transfrom method, and the system function \(H(\omega)\) to compute \(V_L(t)\). Assume \(i_L(0^-)=0\). Verify the result with Matlab.

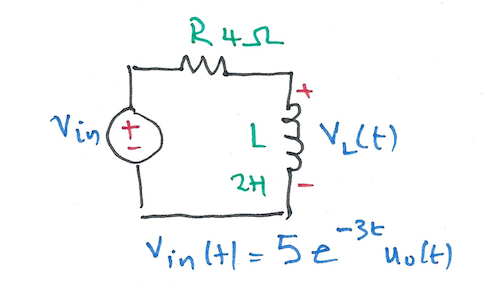
Example 2

MATLAB verification of example 2#

syms t w
H = j*w/(j*w + 2)

H =

(w*1i)/(2 + w*1i)

Vin = fourier(5*exp(-3*t)*heaviside(t),t,w)

Vin =

5/(3 + w*1i)

V_L=simplify(H*Vin)

V_L =

(w*5i)/((2 + w*1i)*(3 + w*1i))

v_L = simplify(ifourier(V_L,w,t))

v_L =

-(5*exp(-3*t)*(sign(t) + 1)*(2*exp(t) - 3))/2

The result is equivalent to:

vout = -5*exp(-3*t)*heaviside(t)*(2*exp(t) - 3)

Which after gathering terms gives

\[v_{\mathrm{out}} = 5\left(3e^{-3t} - 2e^{-2t}\right)u_0(t)\]

Plot result

fplot(v_L,[0,5])
title('Solution to Example 2')
ylabel('v_L(t) [V]')
xlabel('t [s]')
grid
../../_images/b9f5157398d3cc3eca8c81ee22004208e4160bca6594afe8fc185c20f05a98ae.png

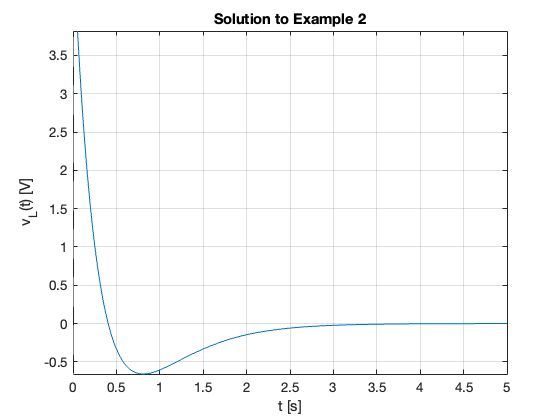
Example 3#

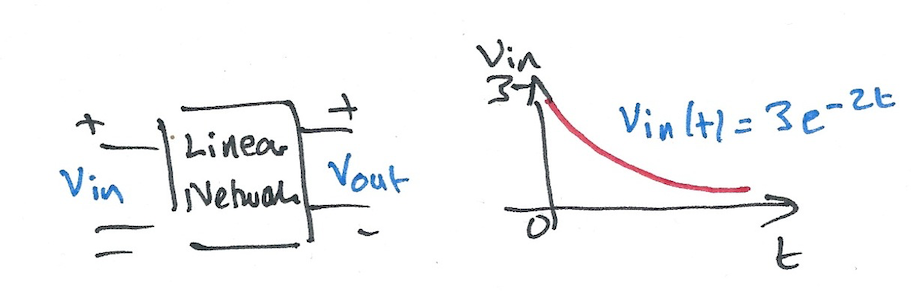
Karris example 8.10: for the linear network shown below, the input-output relationship is:

\[\frac{d}{dt}v_{\mathrm{out}}+4v_{\mathrm{out}}=10v_{\mathrm{in}}\]

where \(v_{\mathrm{in}}=3e^{-2t}\). Use the Fourier transform method, and the system function \(H(\omega)\) to compute the output \(v_{\mathrm{out}}\). Verify the result with Matlab.

Example 3

Matlab verification of example 3#

syms t w
H = 10/(j*w + 4)

H =

10/(4 + w*1i)

Vin = fourier(3*exp(-2*t)*heaviside(t),t,w)

Vin =

3/(2 + w*1i)

Vout=simplify(H*Vin)

Vout =

30/((2 + w*1i)*(4 + w*1i))

vout = simplify(ifourier(Vout,w,t))

vout =

(15*exp(-4*t)*(sign(t) + 1)*(exp(2*t) - 1))/2

The result is equiavlent to:

15*exp(-4*t)*heaviside(t)*(exp(2*t) - 1)

Which after gathering terms gives

\[v_{\mathrm{out}}(t) = 15\left(e^{-2t} - e^{-4t}\right)u_0(t)\]

Plot result

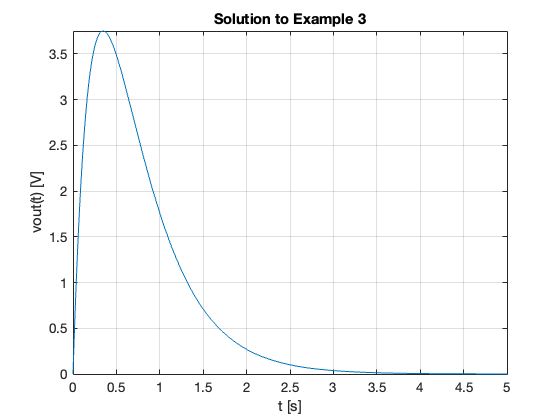
fplot(vout,[0,5])
title('Solution to Example 3')
ylabel('vout(t) [V]')
xlabel('t [s]')
grid
../../_images/ae166cf64ca5363086bbc344c12c8053c78dfbe0312ac1065805378ae18d283e.png

Example 4#

Karris example 8.11: the voltage across a 1 \(\Omega\) resistor is known to be \(V_{R}(t)=3e^{-2t} u_0(t)\). Compute the energy dissipated in the resistor for \(0\lt t\lt\infty\), and verify the result using Parseval’s theorem. Verify the result with Matlab.

Note from tables of integrals

\[\int\frac{1}{a^2 + x^2}\,dx = \frac{1}{a}\arctan\frac{x}{a}+C.\]

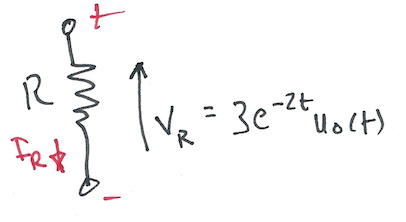
Example 4

MATLAB verification of example 4#

syms t w

Calcuate energy from the time function

Vr = 3*exp(-2*t)*heaviside(t);
R = 1;
Pr = Vr^2/R
Wr = int(Pr,t,0,inf)
double(Wr)

Pr =

9*exp(-4*t)*heaviside(t)^2

Wr =

9/4

ans =
    2.2500

Calculate the energy using Parseval’s theorem

Fw = fourier(Vr,t,w)

Fw =

3/(2 + w*1i)

Fw2 = simplify(abs(Fw)^2)

Fw2 =

9/abs(2 + w*1i)^2

Wr=2/(2*pi)*int(Fw2,w,0,inf)
double(Wr)

Wr =

(51607450253003931*pi)/72057594037927936

ans =
    2.2500

See ft3_ex4.m

Worked Solutions#

MATLAB Solutions#