Homework 1: Revision¶
Problems¶
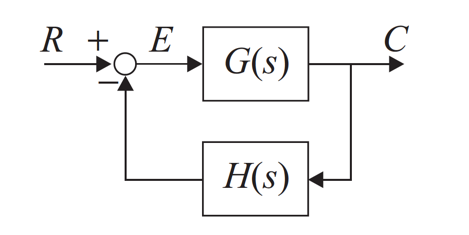
Find the closed-loop characteristic equation of the system illustrated in Figure 1 when:
- \[G(s) = \frac{1}{s+1}$$ when $$H(s) = 1,\;\frac{1}{s+2}\; \mathrm{and}\; s.\]
- \[G(s) = \frac{K(s+2)}{s\left(s^2 + s +1\right)}$$ when $$H(s) = \frac{s+1}{s+10}.\]
A feedback control system has an open-loop transfer function
\[G(s) = \frac{K(s + 2)}{(s + 1)(s - 5)}\]and unity gain feedback. Find the values of \(K\) for which the system is closed-loop stable.
A control system has the root-locus shown in Figure 2. Find the closed-loop poles, natural frequency \(\omega_n\) and gain \(K\) when the damping ratio \(\zeta = 0.0,\;0.1,\;0.5\;\textrm{and}\;1.0\).
What values of gain and damping ratio satisfy the constraints \(2 < \omega_n \le 10\) rads-1.
Is it possible to satisfy the following constraints: rise-time \(T_r \le 0,4\) seconds and peak overshoot \(M_p \le 0.2\) (20%) by adjusting the forward loop gain only?
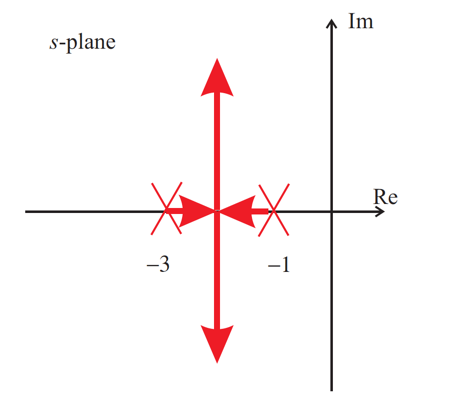Figure 2: Root Locus Diagram for Question 3
Sketch the root-locus diagram for the system of Question 2. Find the value of the open-loop gain that yields closed-loop poles having ideal damping \(\left(\zeta = 1/\sqrt{2}\right)\).
For the system shown in Figure 1
\[G(s) = \frac{1}{sT + 1}\]and
\[H(s) = h.\]Find the steady-state step error of of the closed-loop system and determine its system type number. What is the system type number when \(h = 1\)?
A general second-order closed-loop control system has the transfer function
\[G_c(s)=\frac{b_1 s + b_0}{s^2 + a_1 s + a_0}\]Find suitable values of the parameters \(b_1\), \(b_0\), \(a_1\), and \(a_0\) that provide rise-time \(Tr \le 0.1\) s, settling-time \(T_s \le 0.5\) s, peak-overshoot \(\%\mathrm{OS} \le 20\%\), zero steady-state step error and a ramp error of \(0.01\).