Appendix A — Other Data Representations

Author
Affiliation

Ben Clifford

Welsh Centre for Printing and Coatings

The content of this appendix is intended to expand on what was covered in Introduction to Data Representation.

The text is supported by four short videos which present the material and cover additional information and methods about how data is represented on a microcontroller; these include, two’s complement, binary coded decimal, binary fractions and A.S.C.I.I.

You will find the videos on Canvas on page Two’s complement, BCD, Binary Fractions and A.S.C.I.I.

Contents

A.1 Twos Compliment

A.1.1 Negative Numbers

Up until now, we have only considered positive or unsigned values, how can we handle negative numbers?

An unsigned number itself contains no indication whether it is negative or positive.

A number is said to be signed when the most significant bit (MSB) is used to indicate the sign of the number ‘0’ being used if the number is positive and ‘1’ being used if the number is negative.

Whilst this technique can be used to represent a negative number it is not a practical approach.

Example

Try the following simple sum \(2 + -1 = ?\)

Start with the two numbers

\[\begin{array}{lrr} \mathrm{Addend} & 010 & 2\\ \mathrm{Augend} & 001 & 1\\ \hline \mathrm{Sum} & & \end{array}\]

Chamge the MSB of number 2 to 1 to indicate that it is negative

\[\begin{array}{lrr} \mathrm{Addend} & 0010 & 2 \\ \mathrm{Augend} & 1001 & -1 \\ \hline \mathrm{Sum} & & \end{array}\]

Now add the addend to the augend

\[\begin{array}{lrr} \mathrm{Addend} & 0010 & 2 \\ \mathrm{Augend} & 1001 & -1 \\ \hline \mathrm{Sum} & 1011 & -3 \end{array}\]

The answer comes out as \(-3\) which is clearly wrong. We must use a different approach.

A.1.2 Twos Complement

A more useful way to represent negative numbers is to use the twos complement method.

A binary number has two complements - a ones complement and a twos complement.

  • To get the ones complement, change all 1’s of the unsigned number to 0’s and all 0’s to 1’s, then
  • To get the twos complement add 1 to the ones complement.

Figure A.1 shows the twos complement numbers for all the four bit integers.

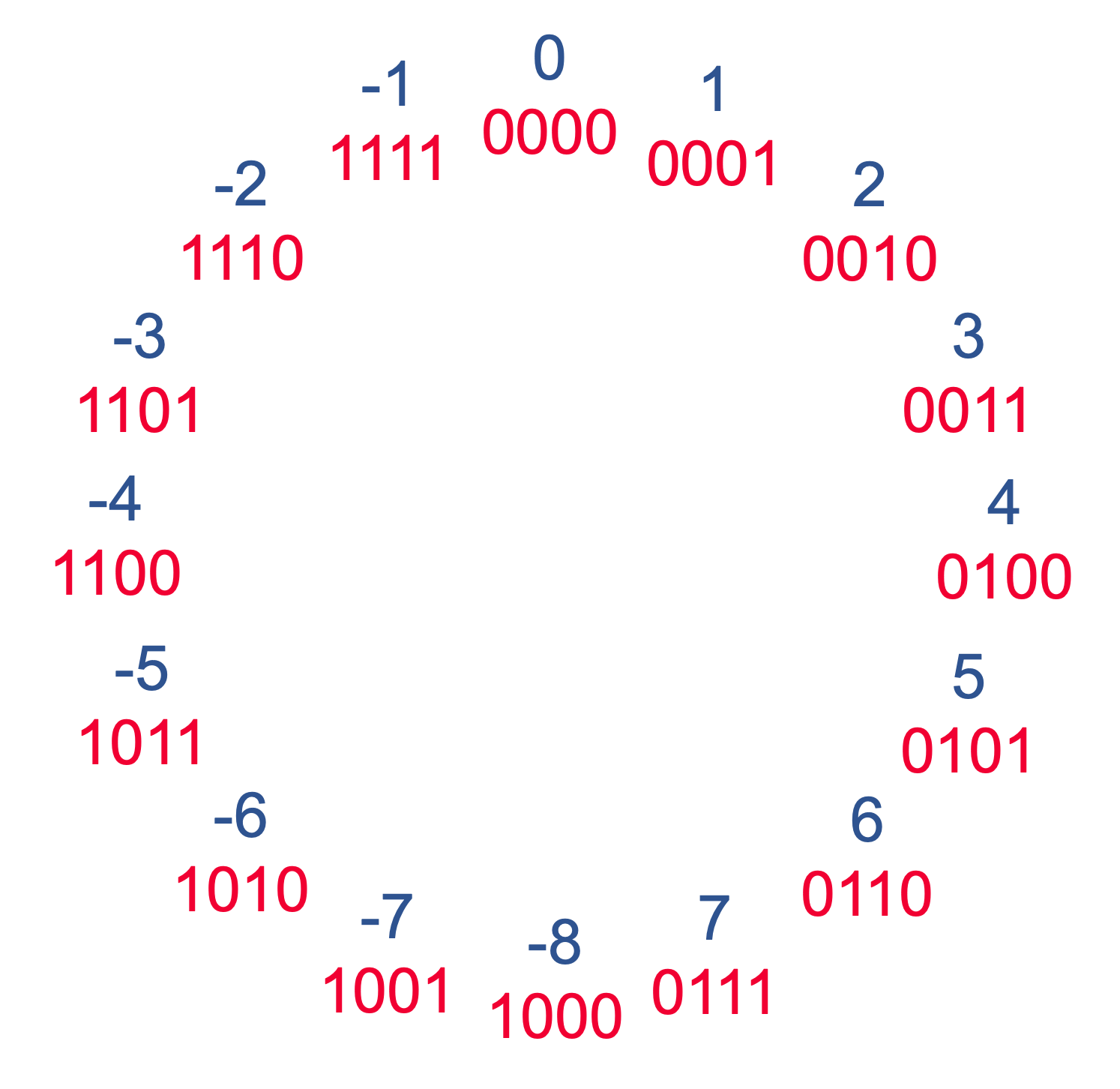
Twos complement.
Figure A.1: Twos complement

Example

Consider the representation of the decimal number \(-1\)

\[\begin{array}{lr} \mathrm{Unsigned\ binary\ number} & 0001\\ \mathrm{Ones\ complement} & 1110\\ \mathrm{Add\ one} & 1\\ \hline \mathrm{Signed\ twos\ complement}& \mathrm{c}1111 \end{array}\]

Now try the addition with the twos complement value (\(1111\)) of \(-1\):

\[\begin{array}{lrr} \mathrm{Addend} & 0010 & 2 \\ \mathrm{Augend} & 1111 & -1 \\ \hline \mathrm{Sum} & \mathrm{c}0001 & -3 \end{array}\]

When performing addition with twos complement, if the MSB is a carry bit, it is dropped.

A.1.3 More examples

Use the twos complement method to represent the decimal number \(-27\)

\[\begin{array}{lr} \mathrm{Unsigned\ value} & 00011011 \\ \mathrm{Ones\ complement} & 11100100 \\ \hline \mathrm{Twos\ complement} & 11100101 \\ \hline \end{array}\]

Check

\[\begin{array}{lrr} \mathrm{Addend} & 00011011 & 27_{10}\\ \mathrm{Augend} & 11100101 & -27_{10}\\ \hline \mathrm{Signed\ twos\ complement}& \mathrm{c}00000000 & 0_{10} \end{array}\]

Use the twos complement method to represent the decimal number \(-84\)

\[\begin{array}{lr} \mathrm{Unsigned\ value} & 01010100 \\ \mathrm{Ones\ complement} & 10101011 \\ \hline \mathrm{Twos\ complement} & 10101100 \\ \hline \end{array}\]

Check

\[\begin{array}{lrr} \mathrm{Addend} & 01010100 & 84_{10}\\ \mathrm{Augend} & 10101100 & -84_{10}\\ \hline \mathrm{Signed\ twos\ complement}& \mathrm{c}00000000 & 0_{10} \end{array}\]

A.2 Binary Coded Decimal (BCD)

Binary Coded Decimal, also known as BCD or 8421 format is another widely used numbering system whereby each decimal digit from 0-9 is individually represented as a 4-bit binary number between 0000 and 1001.

The main advantage of binary coded decimal is that it allows easy conversion between decimal and binary form.

Where is BCD used

  • Calculators
  • Decimal display drivers
  • Digital Clocks
  • PC BIOS to store date and time

Table A.1 shows the codes for the 10 values that are used in BCD coded representations.

Table A.1: Binary Coded Decimal
Decimal BCD Coding
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001

A.2.1 Examples

\(5_{10} ≡ 0101_\textrm{BCD}\)

\(22_{10} ≡ 0010\, 0010_\textrm{BCD}\)

\(86_{10} ≡ 1000\, 0110_\textrm{BCD}\)

\(2020_{10} ≡ 0010\, 0000\, 0010\, 0000_\textrm{BCD}\)

A.2.2 Pros and Cons of Binary Coded Decimal

A.2.2.1 Pros

  • Simple to convert between BCD and decimal values.
  • SLess data loss in floating point calculations.

A.2.2.2 Cons

  • Requires more complex circuitry.

  • Wasteful as only uses 10 out of 16 possible 8-bit representations.

  • Requires more storage than other encoding systems.

    • \(15_{10} = 1111_2 = 0001\, 0101_\textrm{BCD}\)
    • \(255_{10} = 1111\, 1111_2 = 0010\, 0101\, 0101_\textrm{BCD}\)
    • \(8579_{10} = 0010\, 0001\, 1000\, 0011_2 = 1000\, 0101\, 0111\, 1001_\textrm{BCD}\)

A.3 Binary Fractions

A.3.1 Floating Point Numbers

With decimal numbers a decimal point is used to separate the whole and fractional parts of a number. Recalling from {ref}week02 that we represent numbers using a weighted positional notation in which a digit’s value is relative to its position. Figure A.2 illustrates the idea:

Positional notation.
Figure A.2: Positional notation

We use exponentiation of negative powers of the base to represent the fractional part of a number:

\[14.12_{10} = \left(1\times 10^1\right) + \left(4\times 10^0\right) + \left(1\times 10^{-1}\right) + \left(2\times 10^{-2}\right)\]

The idea extends to binary, octal and hexadecimal numbers:

\[\begin{align*} 0000.101_2 &= \left(1\times 2^{-1}\right) + \left(0\times 2^{-2}\right) + \left(1\times 2^{-3}\right) \\ &= \frac{1}{2} + 0\times \frac{1}{4} + \frac{1}{8}\\ &= 0.5 + 0 + 0.125 = 0.625_{10} \end{align*}\]

The representation of octal and hexadecimal numbers is left as an exercise.

A.3.2 Decimal Floating-Point Number Conversion

To convert a decimal fraction (base 10) to a new base (n) the fractional part is repeatedly multiplied by n.

  • The whole number part of the product gives the value at the current power.

  • The decimal part of the product is multiplied by n and repeated until the fractional part of the product is zero.

  • Read the result from top to bottom.

A.3.3 Limitations

Convert \(0.675_{10}\) to binary

0.675 × 2 = 1.35 1

0.35 × 2 = 0.7 0

0.7 × 2 = 1.4 1

0.4 × 2 = 0.8 0

0.8 × 2 = 1.6 1

0.6 × 2 = 1.2 1

0.2 × 2 = 0.4 0

0.4 × 2 = 0.8 0

0.8 × 2 = 1.6 1

Note this is a recurring fraction.

A.3.4 Reality

Modern computers use a special data format called floating point which can be used to approximate decimal numbers to a reasonable precision over a large range. However, floating point numbers need more storage (typically 32 or 64 bits per number) and special hardware to make computation with these values efficient. For microcontrollers, particularly with limited memory and 8-bit data storage, we rarely use floating point arithmetic, or fractions, and rely instead of integer representations.

A.4 ASCII

ASCII. (American Standard Code for Information Interchange) is an encoding format for text developed in the early 1960’s.

The original ASCII format was based on the English alphabet and encodes 128 specified characters into seven-bit binary numbers.

Ninety-five of the encoded characters are printable, including the digits 0 to 9, lowercase letters a to z, uppercase letters A to Z, space, and punctuation symbols.

The remaining 32 non-printing control codes for based around the standards original implementation with Teletype machines – most of these are now obsolete but some are still used including carriage return (\r in C), line feed (\n in C), tab (\t in C).

As microprocessors evolved to 8-bit and higher the ASCII standard has also evolved to use the eighth bit allowing a further 127 characters (extended ASCII).1

The ANSI ASCII table for … is reproduced in Table A.2.

Table A.2: ANSI ASCII Table
Dec Hex Symbol Dec Hex Symbol Dec Hex Symbol Dec Hex Symbol
0 0x00 Null character2 32 0x20 SP 64 0x40 @ 96 0x61 `
1 0x01 Start of heading 32 0x21 ! 65 0x41 A 96 0x61 a
2 0x02 Start of text 34 0x22 " 66 0x42 B 98 0x62 b
3 0x03 End of text 35 0x23 # 67 0x43 C 99 0x63 c
4 0x04 End of Transmission 36 0x24 $ 68 0x44 D 100 0x64 d
5 0x05 Enquiry 37 0x25 % 69 0x45 E 101 0x65 e
6 0x06 Acknowledgement 38 0x26 & 70 0x46 F 102 0x66 f
7 0x07 Bell 39 0x27 ' 71 0x47 G 103 0x67 g
8 0x08 Backspace 40 0x08 ( 72 0x48 H 104 0x68 h
9 0x09 Horizontal tab 41 0x29 ) 73 0x49 I 105 0x69 i
10 0x0A Line feed 42 0x2A * 74 0x4A J 106 0x6A j
11 0x0B Vertical tab 43 0x2B + 75 0x4B K 107 0x6B k
12 0x0C Form feed 44 0x2C , 76 0x4C L 108 0x6C l
13 0x0D Carriage return 45 0x2D - 77 0x4D M 109 0x6D m
14 0x0E Shift out 46 0x2E . 78 0x4E N 110 0x6E n
15 0x0F Shift in 47 0x2F / 79 0x4F O 111 0x6F o
16 0x10 Data link escape 48 0x30 0 80 0x50 P 112 0x70 p
17 0x11 Device control 1 49 0x31 1 81 0x51 Q 113 0x71 q
18 0x02 Device control 2 50 0x32 2 82 0x52 R 114 0x72 r
19 0x13 Device control 3 51 0x33 3 83 0x53 S 115 0x73 s
20 0x14 Device control 4 52 0x34 4 84 0x54 T 116 0x74 t
21 0x15 Negative acknowledgement 53 0x35 5 85 0x55 U 117 0x75 u
22 0x16 Synchronous idle 54 0x36 6 86 0x56 V 118 0x76 v
23 0x17 End of transmission block 55 0x37 7 87 0x57 W 119 0x77 w
24 0x18 Cancel 56 0x38 8 88 0x58 X 120 0x78 x
25 0x19 End of medium 57 0x39 9 89 0x59 Y 121 0x79 y
26 0x1A Substitute 58 0x3A : 90 0x5A Z 122 0x7A z
27 0x1B Escape 59 0x3B ; 91 0x5B [ 123 0x7B {
28 0x1C File separator 60 0x3C < 92 0x5C \ 124 0x7C |
29 0x1D Group separator 61 0x3D = 93 0x4D ] 125 0x7D }
30 0x1E Record separator 62 0x3E > 94 0x5E ^ 126 0x7E ~
31 0x1F Unit separator 63 0x3F ? 95 0x5F _ 127 0x7F Delete

A very useful and useful reference is available as ascii-code.com. See also ASCII Code Chart.

A.4.1 Example

Encode the string “Welcome to Swansea University” in ASCII and give the binary codes that would be used to store this string in computer memory.

A.4.1.1 Solution

Look up the characters and write down the equivalent hexadecimal code. Note, null (\0) is used to terminate the string

'W' = \(87_{10}\) = 0x57 = \(01010111_2\)

'e' = \(101_{10}\) = 0x65 = \(01100101_2\)

'l' = \(108_{10}\) = 0x6C = \(01101011_2\)

'c' = \(99_{10}\) = 0x63 = \(01100011_2\)

'o' = \(111_{10}\) = 0x6F = \(01101111_2\)

'm' = \(109_{10}\) = 0x6D = \(01101101_2\)

'e' = \(108_{10}\) = 0x6C = \(01101011_2\)

' ' = \(108_{10}\) = 0x6C = \(01101011_2\)

't' = \(108_{10}\) = 0x6C = \(01101011_2\)

'o' = \(108_{10}\) = 0x6C = \(01101011_2\)

' ' = \(32_{10}\) = 0x20 = \(00100000_2\)

'S' = \(83_{10}\) = 0x53 = \(01010011_2\)

'w' = \(119_{10}\) = 0x77 = \(01110111_2\)

'a' = \(97_{10}\) = 0x61 = \(01100001_2\)

'n' = \(110_{10}\) = 0x6E = \(01101110_2\)

's' = \(115_{10}\) = 0x73 = \(01110011_2\)

'e' = \(108_{10}\) = 0x6C = \(01101011_2\)

'a' = \(97_{10}\) = 0x61 = \(01100001_2\)

\0 = 0x000 = \(00000000_2\)

The final result (in hexadecimal) is

57
65
6C
63
6F
6D
65
32
74
6E
32
53
77
61
6E
73
65
61
00

  1. As ASCII was only designed to represent English, extended ASCII was developed been used to extend the coding so that displays could print accented European characters, some Greek symbols used in mathematics, and some symbols that could be used to draw boxes on a simple display screen. In order to support the rest of the human languages and alphabets, and for other purposes such as Emojis, ASCII has been extended to a standard called UTF-8. This uses more bytes to represent each character and therefore greatly extends the types of texts that can be stored and manipulated inside a computer.↩︎

  2. the null character (\0 in C) is used in C to mark the end of a string.↩︎

Copyright © 2021-2024 Swansea University. All rights reserved.