Transfer Functions

Second Hour's Agenda

• Transfer Functions

• A Couple of Examples

• Circuit Analysis Using MATLAB LTI Transfer Function Block

• Circuit Simulation Using Simulink Transfer Function Block

Transfer Functions for Circuits

When doing circuit analysis with components defined in the complex frequency domain, the ratio of the output voltage $V_{\mathrm{out}}(s)$ ro the input voltage $V_{\mathrm{in}}(s)$ under zero initial conditions is of great interest. This ratio is known as the voltage transfer function denoted $G_v(s)$:

$$G_v(s) = \frac{V_{\mathrm{out}}(s)}{V_{\mathrm{in}}(s)}$$

Similarly, the ratio of the output current $I_{\mathrm{out}}(s)$ to the input current $I_{\mathrm{in}}(s)$ under zero initial conditions, is called the cuurent transfer function denoted $G_i(s)$:

$$G_i(s) = \frac{I_{\mathrm{out}}(s)}{I_{\mathrm{in}}(s)}$$

In practice, the current transfer function is rarely used, so we will use the voltage transfer function denoted:

$$G(s) = \frac{V_{\mathrm{out}}(s)}{V_{\mathrm{in}}(s)}$$

Example 6

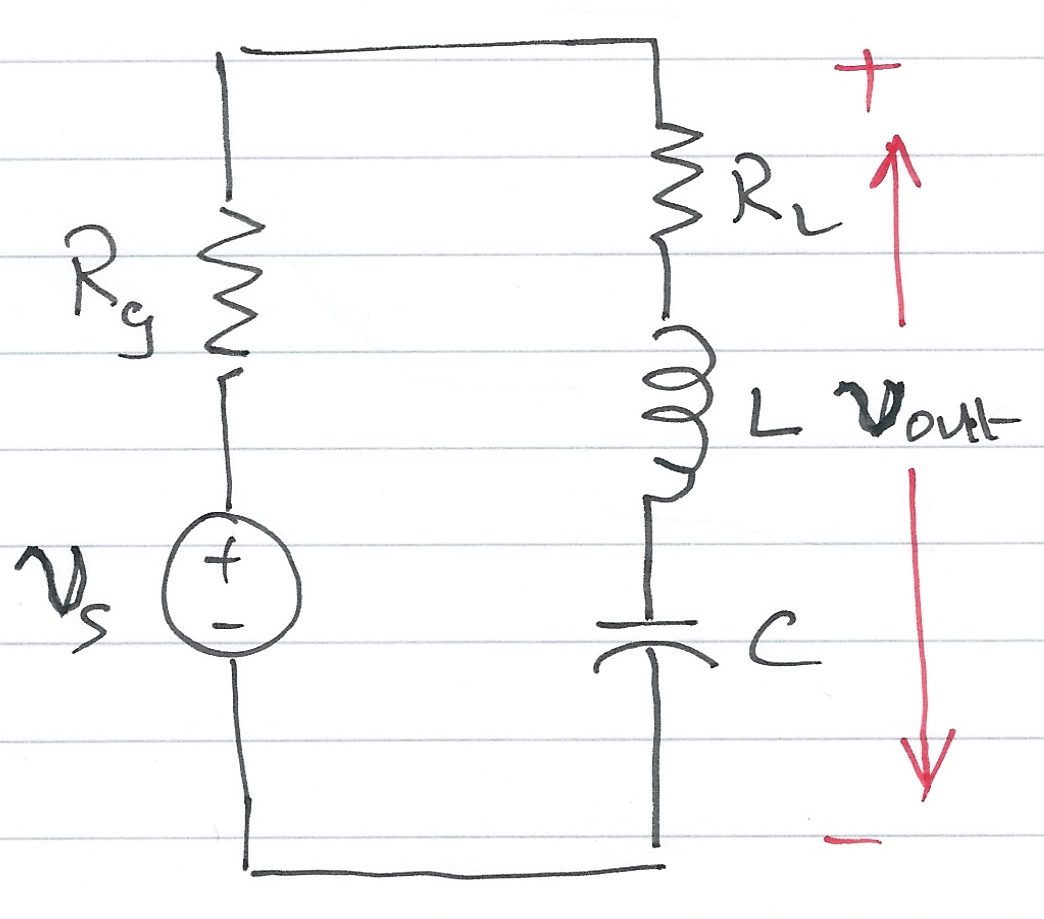
Derive an expression for the transfer function $G(s)$ for the circuit below. In this circuit $R_g$ represents the internal resistance of the applied (voltage) source $v_s$, and $R_L$ represents the resistance of the load that consists of $R_L$, $L$ and $C$.

Sketch of Solution

• Replace $v_s(t)$, $R_g$, $R_L$, $L$ and $C$ by their transformed (complex frequency) equivalents: $V_s(s)$, $R_g$, $R_L$, $sL$ and $1/(sC)$
• Use the Voltage Divider Rule to determine $V_\mathrm{out}(s)$ as a function of $V_s(s)$
• Form $G(s)$ by writing down the ratio $V_\mathrm{out}(s)/V_s(s)$

Worked solution.

Pencast: ex6.pdf - open in Adobe Acrobat Reader.

Answer

$$G(s) = \frac{V_\mathrm{out}(s)}{V_s(s)} = \frac{R_L + sL + 1/sC}{R_g + R_L + sL + 1/sC}.$$

Example 7

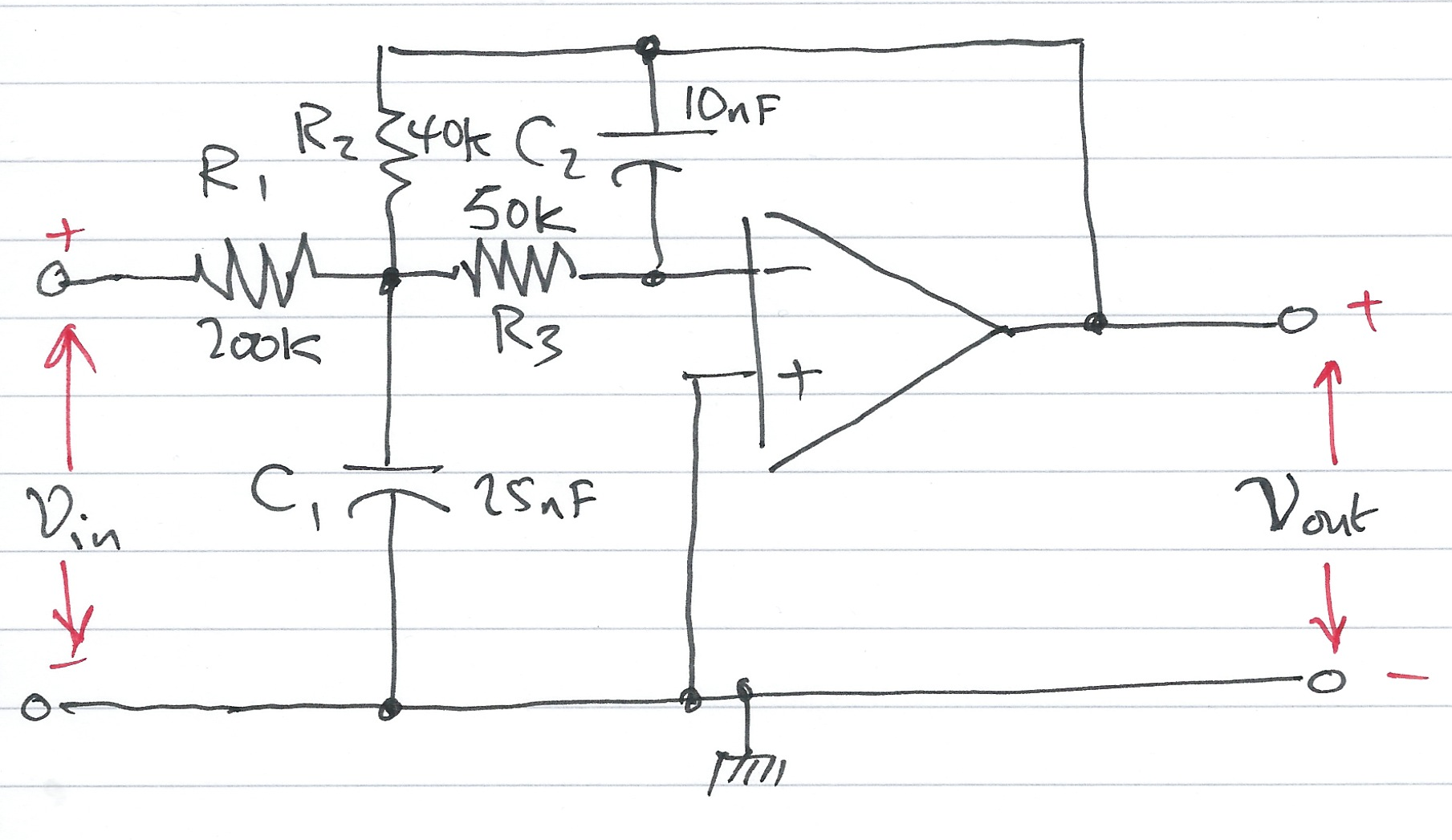
Compute the transfer function for the op-amp circuit shown below in terms of the circuit constants $R_1$, $R_2$, $R_3$, $C_1$ and $C_2$. Then replace the complex variable $s$ with $j\omega$, and the circuit constants with their numerical values and plot the magnitude $\left|G(s)\right| = \left|V_\mathrm{out}(s)/V_\mathrm{in}(s)\right|$ versus radian frequency $\omega$.

Sketch of Solution

• Replace the components and voltages in the circuit diagram with their complex frequency equivalents
• Use nodal analysis to determine the voltages at the nodes either side of the 50K resistor $R_3$
• Note that the voltage at the input to the op-amp is a virtual ground
• Solve for $V_\mathrm{out}(s)$ as a function of $V_\mathrm{in}(s)$
• Form the reciprocal $G(s) = V_\mathrm{out}(s)/V_\mathrm{in}(s)$
• Use MATLAB to calculate the component values, then replace $s$ by $j\omega$.
• Plot $\left|G(j\omega)\right|$ on log-linear "paper"

Worked solution.

Pencast: ex7.pdf - open in Adobe Acrobat Reader.

Answer

$$G(s) = \frac{V_\mathrm{out}(s)}{V_\mathrm{in}(s)} = \frac{-1}{R_1\left(\left(1/R_1 + 1/R_2 + 1/R_3 + sC_1\right)\left(sC_2R_3\right)+1/R_2\right)}.$$

The Matlab Bit

See attached script: solution7.m.

Week 3: Solution 7

syms s;

R1 = 200*10^3; 
R2 = 40*10^3;
R3 = 50*10^3;

C1 = 25*10^(-9);
C2 = 10*10^(-9);

den = R1*((1/R1+ 1/R2 + 1/R3 + s*C1)*(s*R3*C2) + 1/R2);
simplify(den)

 
ans =
 
100*s*((7555786372591433*s)/302231454903657293676544 + 1/20000) + 5
 

Result is: 100*s*((7555786372591433*s)/302231454903657293676544 + 1/20000) + 5

Simplify coefficients of s in denominator

format long
denG = sym2poly(ans)

denG =

   0.000002500000000   0.005000000000000   5.000000000000000

numG = -1;

Plot

For convenience, define coefficients $a$ and $b$:

a = denG(1);
b = denG(2);

w = 1:10:10000;

$$G(j\omega) = \frac{-1}{a\omega^2 - jb\omega + 5}$$

Gs = -1./(a*w.^2 - j.*b.*w + denG(3));

semilogx(w, abs(Gs))
xlabel('Radian frequency w (rad/s')
ylabel('|Vout/Vin|')
title('Magnitude Vout/Vin vs. Radian Frequency')
grid

Using Transfer Functions in Matlab for System Analysis

Please use the file tf_matlab.m to explore the Transfer Function features provide by Matlab. Use the publish option to generate a nicely formatted document.

Using Transfer Functions in Simulink for System Simulation

The Simulink transfer function (Transfer Fcn) block shown above implements a transfer function representing a general input output function

$$G(s) = \frac{N(s)}{D(s)}$$

that it is not specific nor restricted to circuit analysis. It can, however be used in modelling and simulation studies.

Example

Recast Example 7 as a MATLAB problem using the LTI Transfer Function block.

For simplicity use parameters $R_1 = R_2 = R_3 = 1\; \Omega$, and $C_1 = C_2 = 1\;\mathrm{F}$.

Calculate the step response using the LTI functions.

Verify the result with Simulink.

The Matlab solution: example8.m

MATLAB Solution

From a previous analysis the transfer function is:

$$G(s) = \frac{V_\mathrm{out}}{V_\mathrm{in}} = \frac{-1}{R_1\left[(1/R_1 + 1/R_2 + 1/R_3 + sC_1)(sR_3C_2) + 1/R_2\right]}$$

so substituting the component values we get:

$$G(s) = \frac{V_\mathrm{out}}{V_\mathrm{in}} = \frac{-1}{s^2 + 3s + 1}$$

We can find the step response by letting $v_\mathrm{in}(t) = u_0(t)$ so that $V_\mathrm{in}(s)=1/s$ then

$$V_\mathrm{out}(s) = \frac{-1}{s^2 + 3s + 1}.\frac{1}{s}$$

We can solve this by partial fraction expansion and inverse Laplace transform as is done in the text book with the help of Matlab's residue function.

Here, however we'll use the LTI block that was introduced in the lecture.

Define the circuit as a transfer function

G = tf([-1],[1 3 1])

G =
 
       -1
  -------------
  s^2 + 3 s + 1
 
Continuous-time transfer function.

step response is then:

step(G)

Simples!

Simulink model

See example_8.slx

open example_8

Result

Let's go a bit further by finding the frequency response:

bode(G)