Using Laplace Transforms for Circuit Analysis

First Hour's Agenda

We look at applications of the Laplace Transform for

• Circuit transformation from Time to Complex Frequency

• Complex impedance

• Complex admittance

Circuit Transformation from Time to Complex Frequency

Resistive Network - Time Domain

Resistive Network - Complex Frequency Domain

Inductive Network - Time Domain

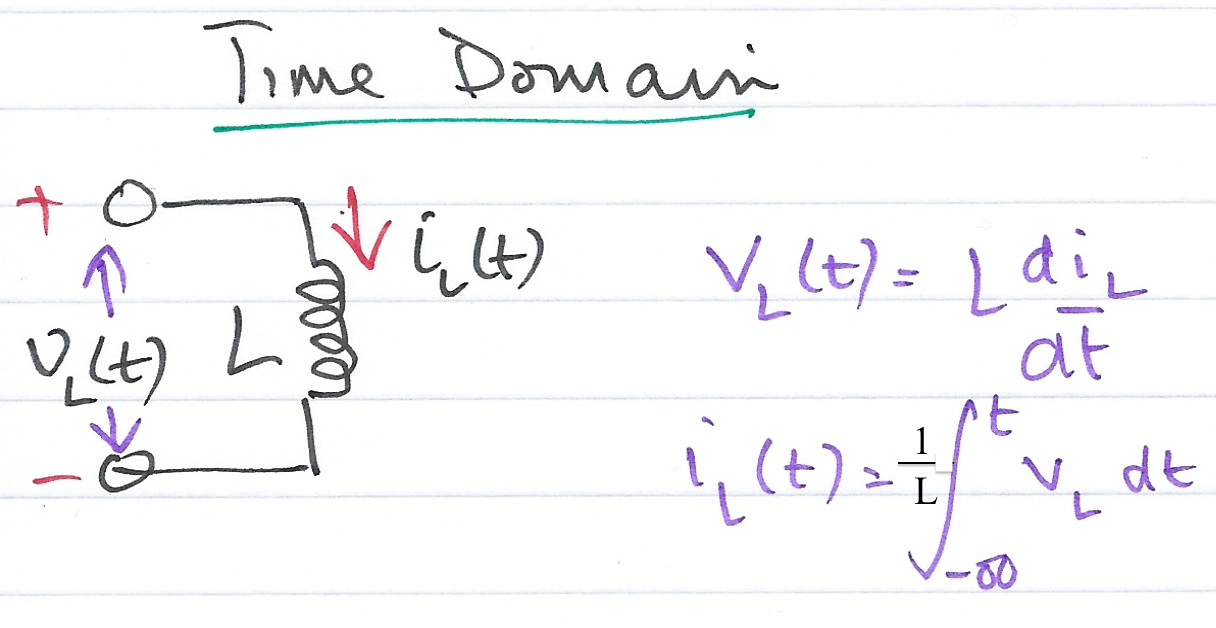
Inductive Network - Complex Frequency Domain

Capacitive Network - Time Domain

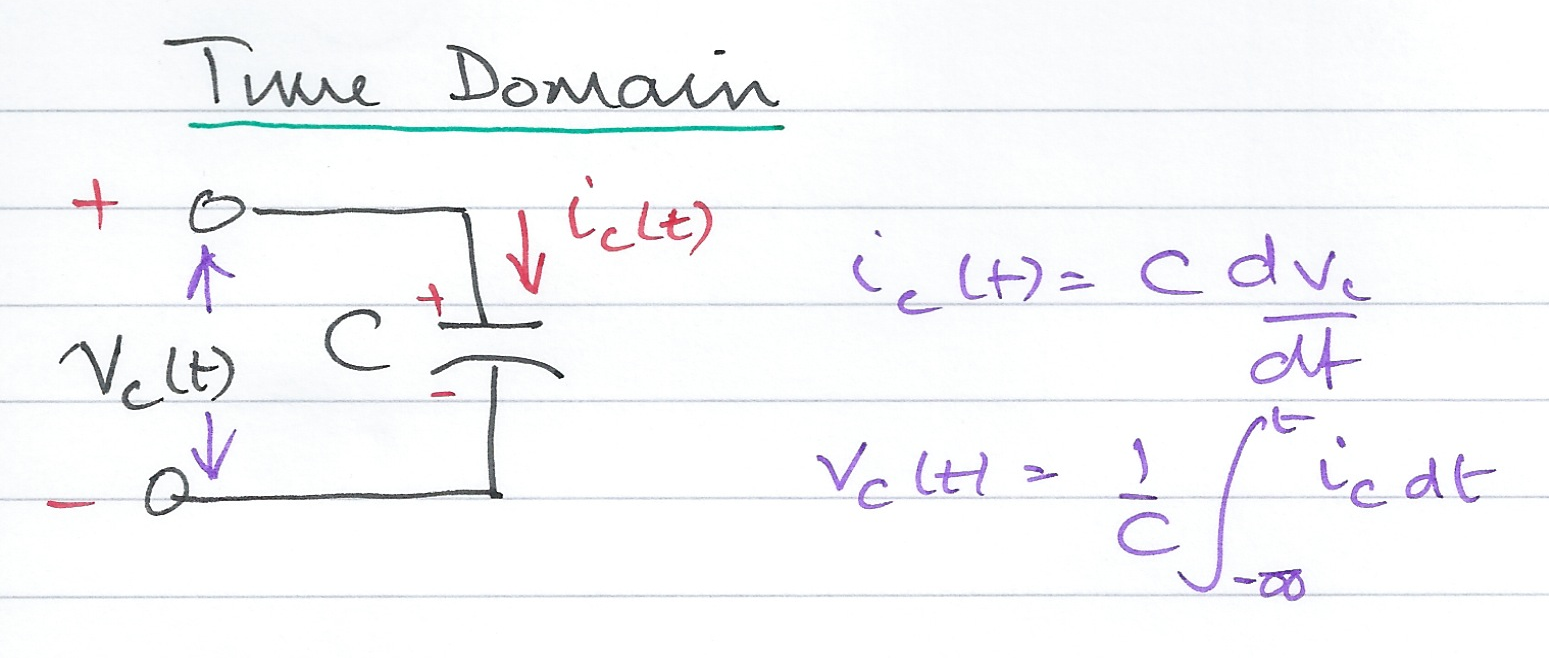
Capacitive Network - Complex Frequency Domain

Examples

Example 1

Use the Laplace transform method and apply Kirchoff's Current Law (KCL) to find the voltage $v_c(t)$ across the capacitor for the circuit below given that $v_c(0^-) = 6$ V.

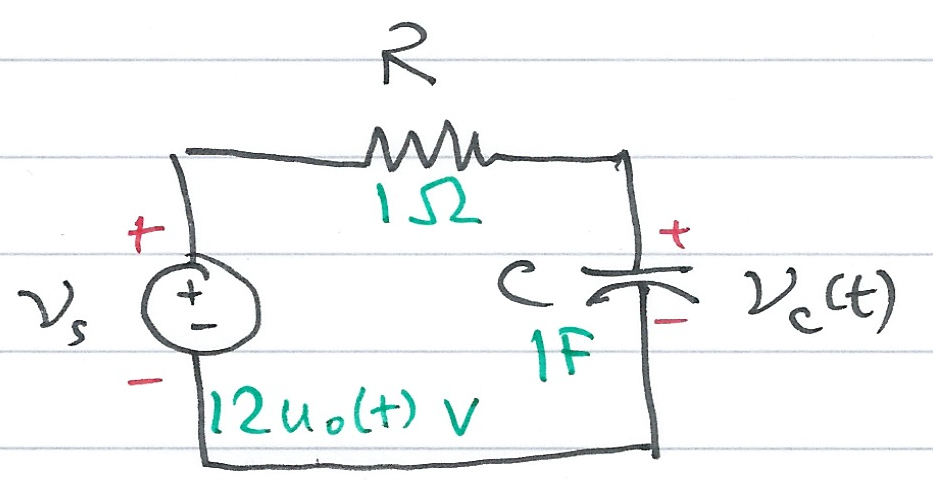
Example 2

Use the Laplace transform method and apply Kirchoff's Voltage Law (KVL) to find the voltage $v_c(t)$ across the capacitor for the circuit below given that $v_c(0^-) = 6$ V.

Example 3

In the circuit below, switch $S_1$ closes at $t=0$, while at the same time, switch $S_2$ opens. Use the Laplace transform method to find $v_{\mathrm{out}}(t)$ for $t > 0$.

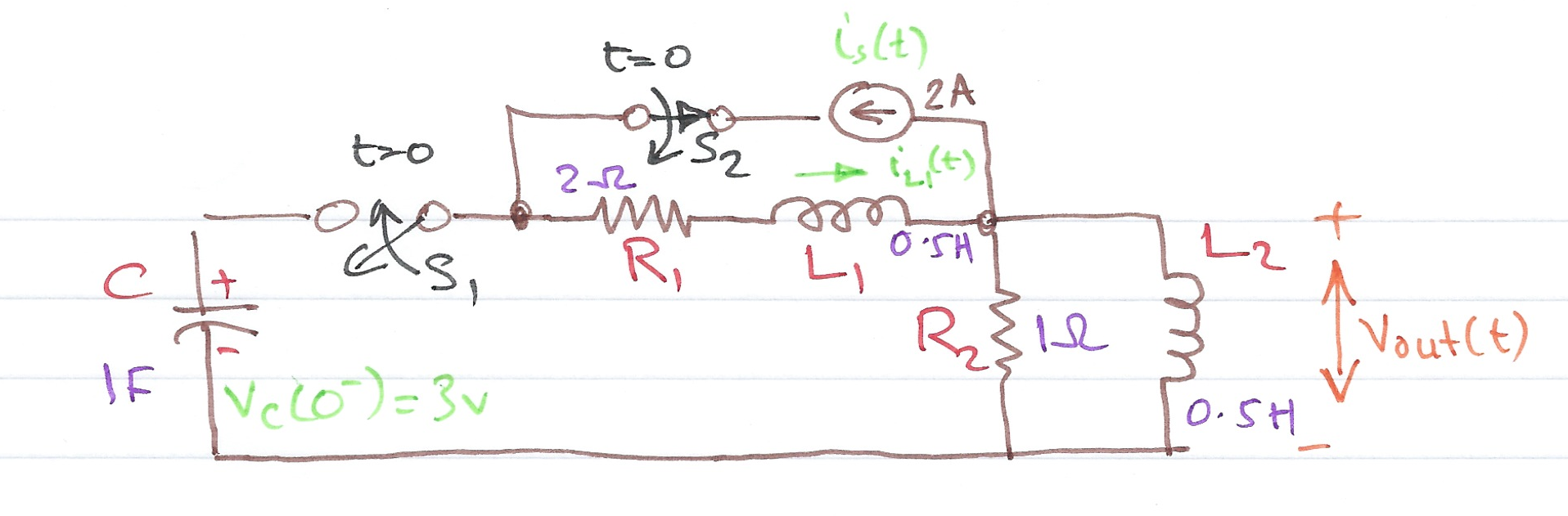
Show with the assistance of MATLAB (See solution3.m) that the solution is

$$V_{\mathrm{out}}=\left(1.36e^{-6.57t}+0.64e^{-0.715t}\cos 0.316t - 1.84e^{-0.715t}\sin 0.316t\right)u_0(t)$$

and plot the result.

Solution to Example 3

We will use a combination of pen-and-paper and MATLAB to solve this.

1. Equivalent Circuit

Draw equivalent circuit at $t=0$

2. Transform model

Convert to transforms

3. Determine equation

Determine equation for $V_{\rm out}(s)$.

4. Complete solution in MATLAB

In the lecture we showed that after simplification for Example 3

$$V_{\mathrm{out}}=\frac{2s(s+3)}{s^3 + 8s^2 + 10s + 4}$$

We will use MATLAB to factorize the denominator $D(s)$ of the equation into a linear and a quadratic factor.

Find roots of Denominator D(s)

r = roots([1, 8, 10, 4])

r =

  -6.5708 + 0.0000i
  -0.7146 + 0.3132i
  -0.7146 - 0.3132i

Find quadratic form

syms s t
y = expand((s - r(2))*(s - r(3)))

 
y =
 
s^2 + (804595903579775*s)/562949953421312 + 3086772113315577969665007046981/5070602400912917605986812821504
 

Simplify coefficients of s

y = sym2poly(y)

y =

    1.0000    1.4292    0.6088

Complete the Square

Plot result

t=0:0.01:10;
Vout = 1.36.*exp(r(1).*t)+0.64.*exp(real(r(2)).*t).*cos(imag(r(2)).*t)-1.84.*exp(real(r(3)).*t).*sin(-imag(r(3)).*t);
plot(t, Vout); grid
title('Plot of Vout(t) for the circuit of Example 3')
ylabel('Vout(t) V'),xlabel('Time t s')

Worked Solution: Example 3

File Pencast: example3.pdf - Download and open in Adobe Accrobat Reader.

The attached "PenCast" works through the solution to Example 3 by hand. It's quite a complex, error-prone (as you will see!) calculation that needs careful attention to detail. This in itself gives justification to my belief that you should use computers wherever possible.

Please note, the PenCast takes around 39 minutes (I said it was a complex calculation) but you can fast forward and replay any part of it.

Alternative solution using transfer functions

Vout = tf(2*conv([1, 0],[1, 3]),[1, 8, 10, 4])

Vout =
 
       2 s^2 + 6 s
  ----------------------
  s^3 + 8 s^2 + 10 s + 4
 
Continuous-time transfer function.

impulse(Vout)

Complex Impedance Z(s)

Consider the $s$-domain RLC series circuit, wehere the initial conditions are assumed to be zero.

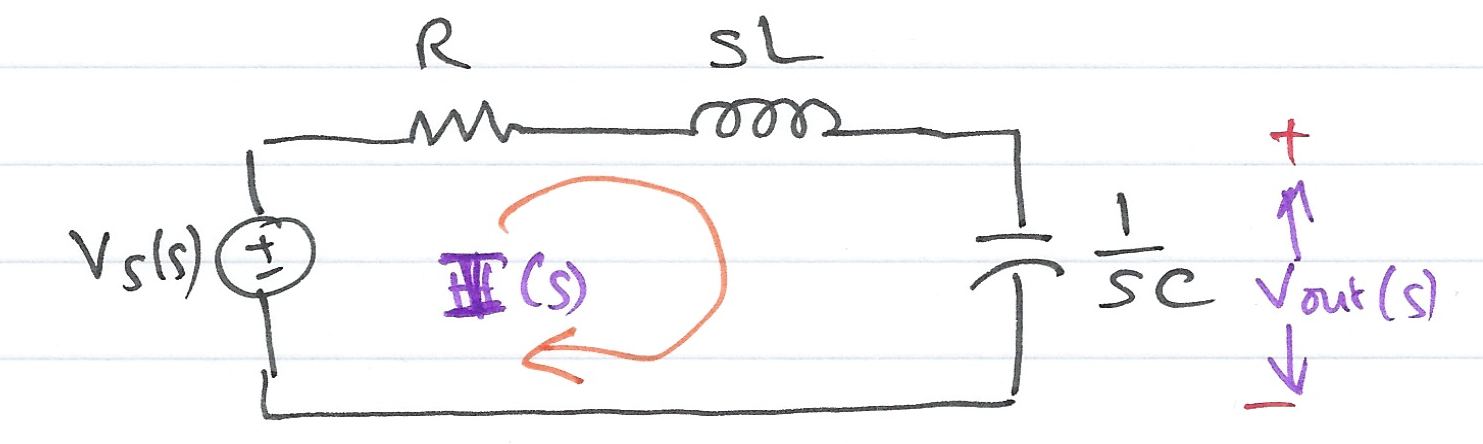
For this circuit, the sum

$$R + sL + \frac{1}{sC}$$

represents that total opposition to current flow. Then,

$$I(s) = \frac{V_s(s)}{R + sL + 1/(sC)}$$

and defining the ratio $V_s(s)/I(s)$ as $Z(s)$, we obtain

$$Z(s) = \frac{V_s(s)}{I(s)} = R + sL + \frac{1}{sC}$$

The $s$-domain current $I(s)$ can be found from

$$I(s) = \frac{V_s(s)}{Z(s)}$$

where

$$Z(s) = R + sL + \frac{1}{sC}.$$

Since $s = \sigma + j\omega$ is a complex number, $Z(s)$ is also complex and is known as the complex input impedance of this RLC series circuit.

Exercise

Use the previous result to give an expression for $V_c(s)$

Example 4

For the network shown below, all the complex impedence values are given in $\Omega$ (ohms).

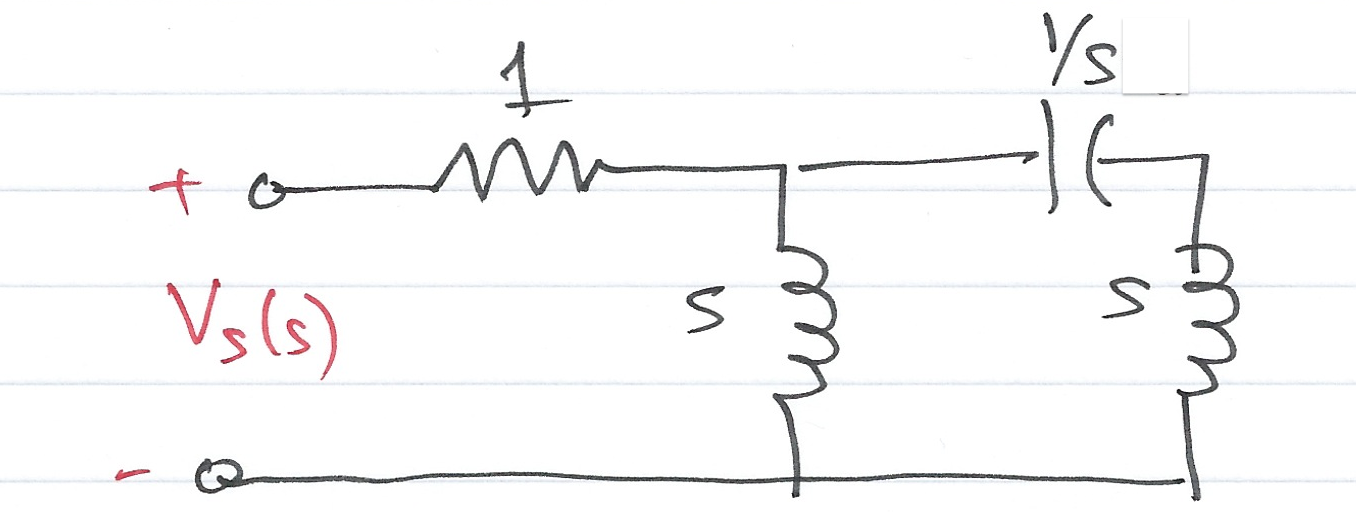
Find $Z(s)$ using:

1. nodal analysis
2. successive combinations of series and parallel impedances

Solutions: Pencasts ex4_1.pdf and ex4_1.pdf – open in Adobe Acrobat.

Complex Admittance Y(s)

Consider the $s$-domain GLC parallel circuit shown below where the initial conditions are zero.

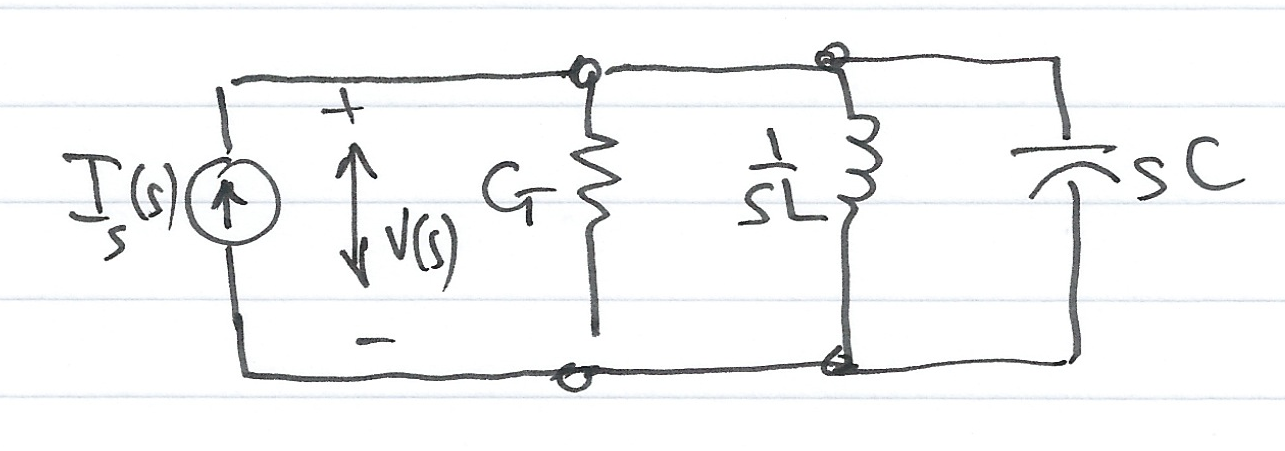
For this circuit

$$GV(s)+ \frac{1}{sL}V(s) + sCV(s) = I_s(s)$$

$$\left(G+ \frac{1}{sL} + sC\right)V(s) = I_s(s)$$

Defining the ratio $I_s(s)/V(s)$ as $Y(s)$ we obtain

$$Y(s)=\frac{I_s(s)}{V(s)} = G+ \frac{1}{sL} + sC = \frac{1}{Z(s)}$$

The $s$-domain voltage $V(s)$ can be found from

$$V(s) = \frac{I_s(s)}{Y(s)}$$

where

$$Y(s) = G + \frac{1}{sL} + sC.$$

$Y(s)$ is complex and is known as the complex input admittance of this GLC parallel circuit.

Example 5 - Do It Yourself

Compute $Z(s)$ and $Y(s)$ for the circuit shown below. All impedence values are in $\Omega$ (ohms). Verify your answers with MATLAB.

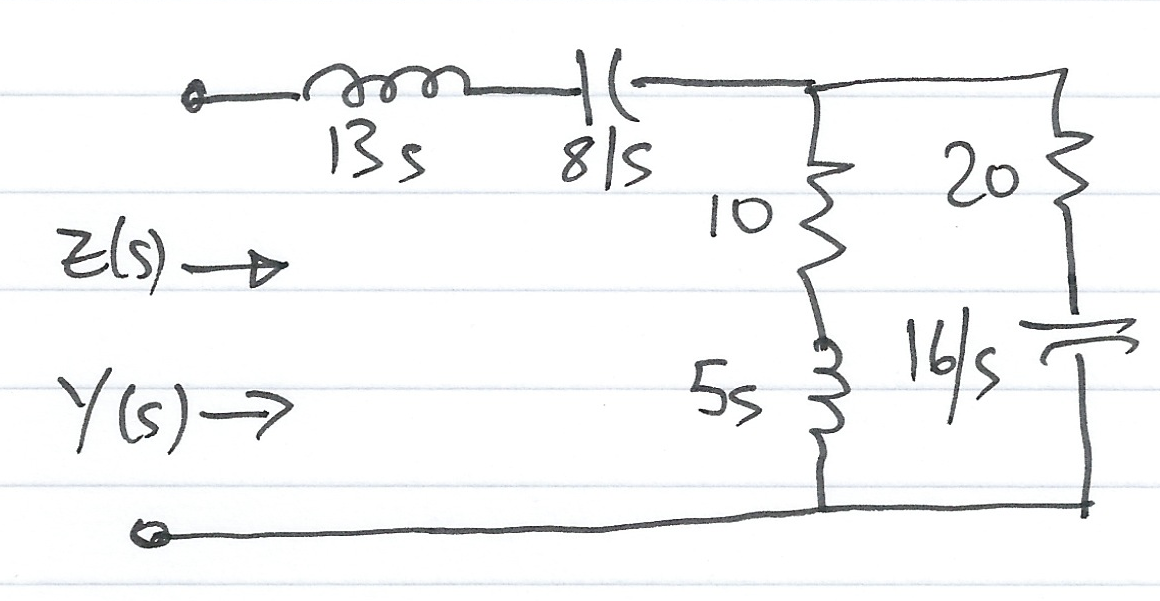
Answer 5

$$Z(s) = \frac{65s^4 + 490s^3 + 528s^2 + 400s + 128}{s(5s^2 + 30s + 16)}$$

$$Y(s) = \frac{1}{Z(s)} = \frac{s(5s^2 + 30s + 16)}{65s^4 + 490s^3 + 528s^2 + 400s + 128}$$

Matlab verification: solution5.m

Example 5: Verification of Solution

syms s;

z1 = 13*s + 8/s;
z2 = 5*s + 10;
z3 = 20 + 16/s;

z = z1 + z2 * z3 /(z2 + z3)

 
z =
 
13*s + 8/s + ((5*s + 10)*(16/s + 20))/(5*s + 16/s + 30)
 

z10 = simplify(z)

 
z10 =
 
(65*s^4 + 490*s^3 + 528*s^2 + 400*s + 128)/(s*(5*s^2 + 30*s + 16))
 

pretty(z10)

    4        3        2
65 s  + 490 s  + 528 s  + 400 s + 128
-------------------------------------
               2
         s (5 s  + 30 s + 16)

Admittance

y10 = 1/z10;
pretty(y10)

               2
         s (5 s  + 30 s + 16)
-------------------------------------
    4        3        2
65 s  + 490 s  + 528 s  + 400 s + 128