Elementary Signals

Consider this circuit:

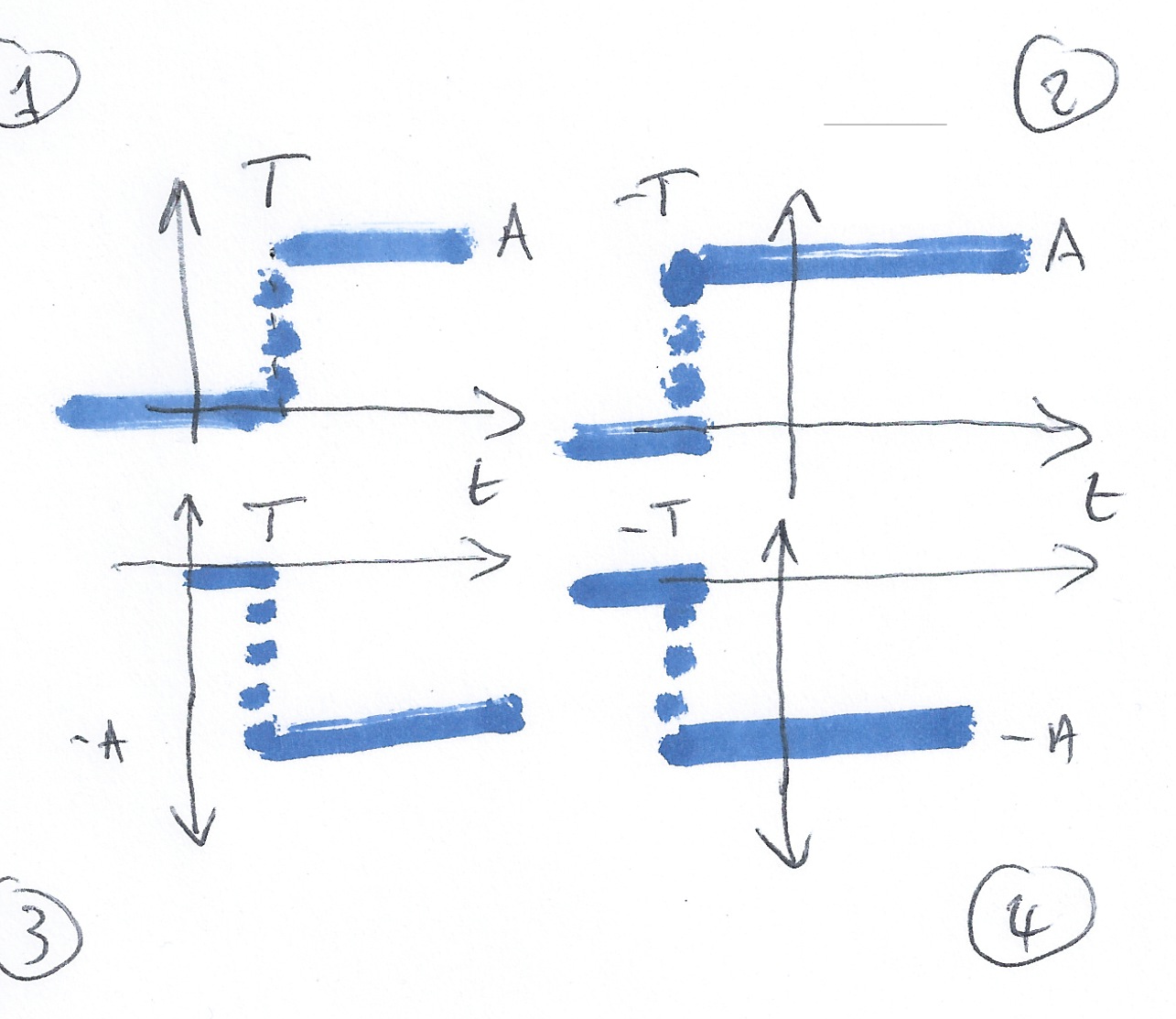
Q1: What happens before $t=0$?

1. $v_{\mathrm{out}} = \mathrm{undefined}$
2. $v_{\mathrm{out}} = 0$
3. $v_{\mathrm{out}} = V_s$
4. $v_{\mathrm{out}} = 1/2$
5. $v_{\mathrm{out}} = \infty$

Q2: What happens after $t=0$?

1. $v_{\mathrm{out}} = \mathrm{undefined}$
2. $v_{\mathrm{out}} = 0$
3. $v_{\mathrm{out}} = V_s$
4. $v_{\mathrm{out}} = 1/2$
5. $v_{\mathrm{out}} = \infty$

Q3: What happens at $t=0$?

1. $v_{\mathrm{out}} = \mathrm{undefined}$
2. $v_{\mathrm{out}} = 0$
3. $v_{\mathrm{out}} = V_s$
4. $v_{\mathrm{out}} = 1/2$
5. $v_{\mathrm{out}} = \infty$

Q4: What does the response of $V_{\mathrm{out}}$ look like? Circle the picture you think is correct on your handout.

1:

2:

3:

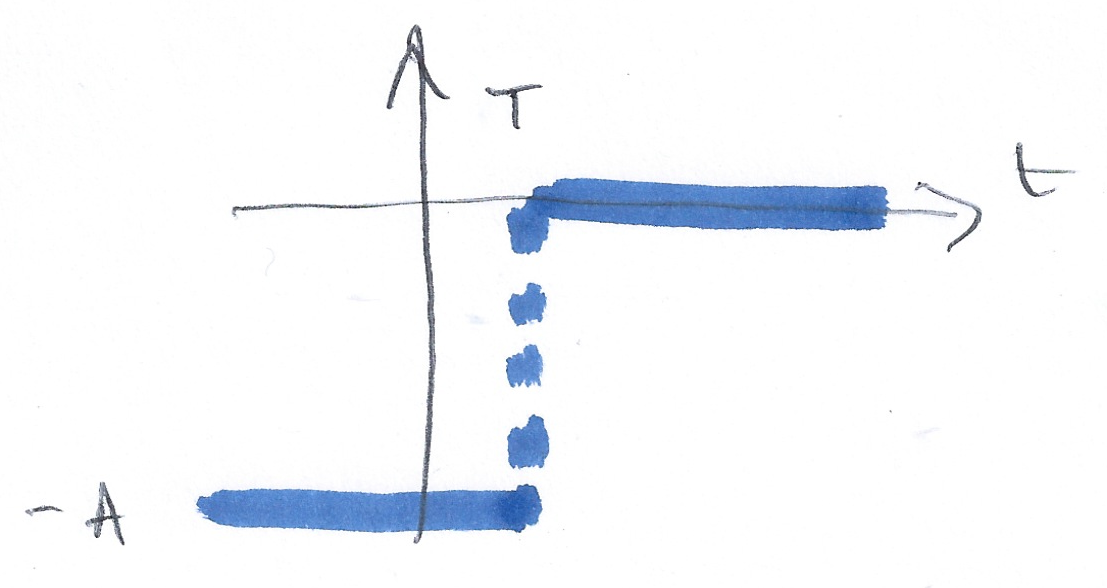
4: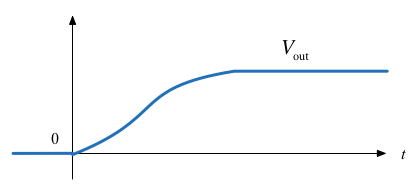

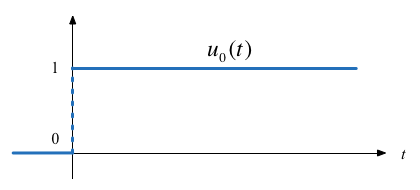
The Unit Step Function

$${u_0}(t) = \left\{ {\begin{array}{*{20}{c}} {0\quad t < 0}\\ {1\quad t > 0} \end{array}} \right.$$

In Matlab

In Matlab, we use the heaviside function (Named after Oliver Heaviside).

syms t
ezplot(heaviside(t),[-1,1])
heaviside(0)

ans =

    0.5000

See: heaviside_function.m

Note that, so it can be plotted, Matlab defines the heaviside function slightly differently from the mathematically ideal unit step:

$$\mathrm{heaviside}(t) = \left\{ {\begin{array}{*{20}{c}} {0\quad t < 0}\\ {1/2\quad t = 0}\\ {1\quad t > 0} \end{array}} \right.$$

Circuit Revisited

Consider the network shown below, where the switch is closed at time $t=T$.

Express the output voltage $v_{\mathrm{out}}$ as a function of the unit step function, and sketch the appropriate waveform.

Simple Signal Operations

Amplitude Scaling

Sketch $Au_0(t)$ and $-Au_0(t)$

Time Reversal

Sketch $u_0(-t)$

Time Delay and Advance

Sketch $u_0(t-T)$ and $u_0(t+T)$

Examples

Example 1

Which of these signals represents $-Au_0(t+T)$?

-> Open Poll

Example 2

What is represented by

-> Open Poll

1. $-Au_0(t + T)$
2. $-Au_0(-t + T)$
3. $-Au_0(-t - T)$
4. $-Au_0(t-T)$

Synthesis of Signals from Unit Step

Unit step functions can be used to represent other time-varying functions such as rectangular pulses, square waves and triangular pulses.

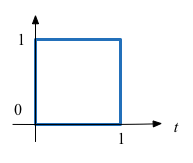
Synthesize Rectangular Pulse

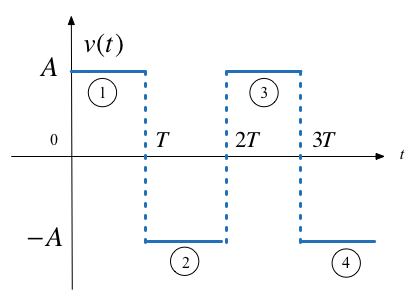
Synthesize Square Wave

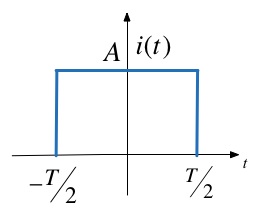
Synthesize Symmetric Rectangular Pulse

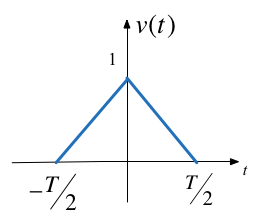
Synthesize Symmetric Triangular Pulse

The Ramp Function

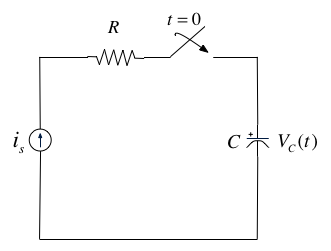
In the circuit shown above $i_s$ is a constant current source and the switch is closed at time $t=0$.

Show that the voltage across the capacitor can be represented as

$$v_C(t)=\frac{i_s}{C}t u_0(t)$$

and sketch the wave form.

The unit ramp function is defined as

$$u_1(t) = \int_{-\infty}^{t}u_0(\tau)d\tau$$

so

$${u_1}(t) = \left\{ {\begin{array}{*{20}{c}} {0\quad t < 0}\\ {t\quad t \ge 0} \end{array}} \right.$$

and

$$u_0(t) = \frac{d }{dt}u_1(t)$$

Note

Higher order functions of $t$ can be generated by the repeated integration of the unit step function.

For future reference, you should determine $u_2(t)$, $u_3(t)$ and $u_n(t)$ for yourself and make a note of the general rule:

$$u_{n-1} = \frac{1}{n}\frac{d}{dt}u_n(t)$$

Details are given in equations 1.26—1.29 in the textbook.

The Dirac Delta Function

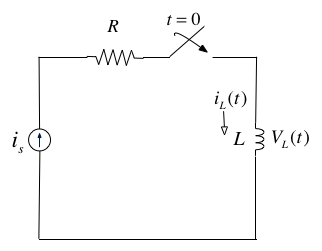
In the circuit shown above, the switch is closed at time $t=0$ and $i_L(t)=0$ for $t<0$. Express the inductor current $i_L(t)$ in terms of the unit step function and hence derive an expression for $v_L(t)$.

Notes

To solve this problem we need to invent a function that represents the derivative of the unit step function. This function is called $\delta(t)$ or the dirac delta function (named after Paul Dirac).

The delta function

The unit impulse or the delta function, denoted as $\delta(t)$, is the derivative of the unit step.

This function is tricky because $u_0(t)$ is discontinuous at $t=0$ but it must have the properties

$$\int_{-\infty}^{t}\delta(\tau)d\tau = u_0(t)$$

and

$\delta(t) = 0$ for all $t\ne 0$.

Sketch of the delta function

Important properties of the delta function

Sampling Property

The sampling property of the delta function states that

$$f(t)\delta(t-a) = f(a)\delta(t-a)$$

or, when $a = 0$,

$$f(t)\delta(t) = f(0)\delta(t)$$

Multiplication of any function $f(t)$ by the delta function $\delta(t)$ results in sampling the function at the time instants for which the delta function is not zero.

The study of descrete-time (sampled) systems is based on this property.

You should work through the proof for youself.

Sifting Property

The sifting property of the delta function states that

$$\int_{-\infty}^{\infty}f(t)\delta(t-\alpha)dt=f(\alpha)$$

That is, if multiply any function $f(t)$ by $\delta(t-\alpha)$, and integrate from $-\infty$ to $+\infty$, we will get the value of $f(t)$ evaluated at $t=\alpha.$

You should also work through the proof for yourself.

Higher Order Delta Fuctions

the nth-order delta function is defined as the nth derivative of $u_0(t)$, that is

$$\delta^n(t)=\frac{d^n}{dt^n}[u_0(t)]$$

The function $\delta'(t)$ is called the doublet, $\delta''(t)$ is called the triplet and so on.

By a procedure similar to the derivation of the sampling property we can show that

$$f(t)\delta'(t-a)=f(a)\delta'(t-a)-f'(t)\delta(t-a)$$

Also, derivation of the sifting property can be extended to show that

$$\int_{-\infty}^{\infty}f(t)\delta^n(t-\alpha)dt = {\left. {{{( - 1)}^n}\frac{{{d^n}}}{{d{t^n}}}[f(t)]} \right|_{t = \alpha }}$$

Examples

Example 3

Evaluate the following expressions

$$3t^4\delta(t-1) $$

</pre></li>

$$\int_{-\infty}^{\infty}t\delta(t-2)dt$$

</pre></li>

$$t^2\delta'(t-3)$$

</pre></li>
</ol>

Example 4

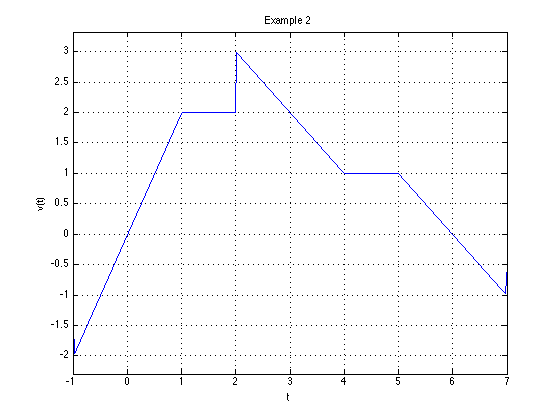
(1) Express the voltage waveform $v(t)$ shown above as a sum of unit step functions for the time interval $-1 < t < 7$ s

</pre></li>

Using the result of part (1), compute the derivative of $v(t)$ and sketch its waveform.

</pre></li>
</ol>

Lab Work

In the second lab, a week on Monday, we will solve Example 2 using Matlab/Simulink following the procedure given between pages 1-17 and 1-22 of the textbook. We will also explore the heaviside and dirac functions.

Answers to in-class questions

Mathematically

Q1. $v_{\mathrm{out}} = 0$ when $-\infty < t < 0$ (answer 2)

Q2. $v_{\mathrm{out}} = V_s$ when $0 < t < \infty$ (answer 3)

Q3. $v_{\mathrm{out}} = \mathrm{undefined}$ when $t=0$ (answer 1)

$V_{\mathrm{out}}$ jumps from $0$ to $V_s$ instantanously when the switch is closed. We call this a discontinuous signal!

Q4: The correct image is: